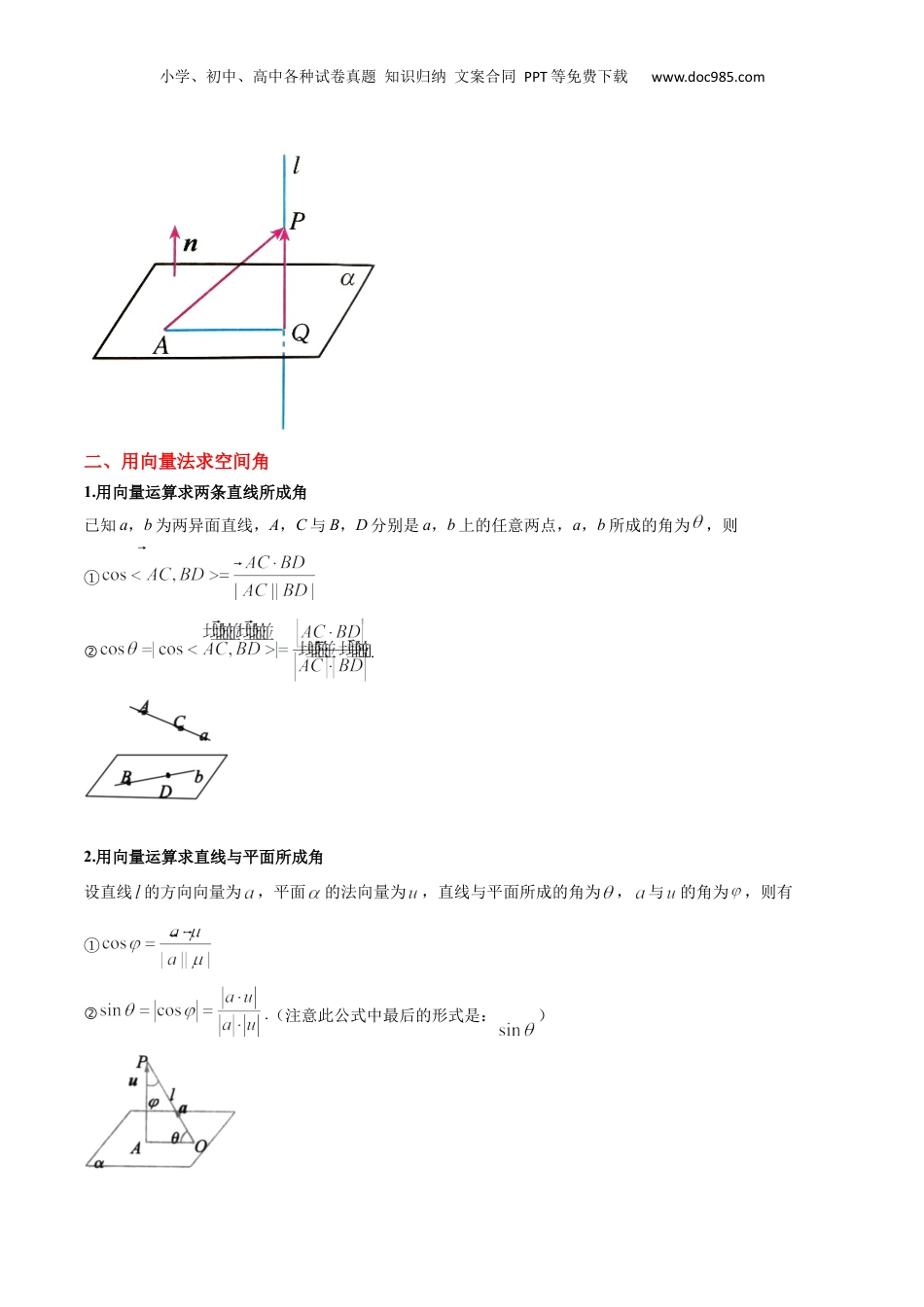
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2024年高二数学暑假预习（人教A版2019选择性必修第一册）预习04讲用空间向量研究夹角、距离问题（精讲+精练）①利用空间向量求异面直线所成角②利用空间向量求线面角③利用空间向量求面面角④利用空间向量求点到线、点到面距离一、用向量法求空间距离1.点到直线的距离已知直线的单位方向向量为，是直线上的定点，是直线外一点.设，则向量在直线上的投影向量，在中，由勾股定理得：2.点到平面的距离如图，已知平面的法向量为，是平面内的定点，是平面外一点.过点作平面的垂线，交平面于点，则是直线的方向向量，且点到平面的距离就是在直线上的投影向量的长度.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com二、用向量法求空间角1.用向量运算求两条直线所成角已知a，b为两异面直线，A，C与B，D分别是a，b上的任意两点，a，b所成的角为，则①②.2.用向量运算求直线与平面所成角设直线的方向向量为，平面的法向量为，直线与平面所成的角为，与的角为，则有①②.（注意此公式中最后的形式是：）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3.用向量运算求平面与平面的夹角如图，若于A，于B，平面PAB交于E，则∠AEB为二面角的平面角，∠AEB+∠APB=180°.若分别为面，的法向量①②根据图形判断二面角为锐二面角还是顿二面角；若二面角为锐二面角（取正），则；若二面角为顿二面角（取负），则；①利用空间向量求异面直线所成角策略方法用向量法求异面直线所成角的一般步骤【题型精练】一、单选题小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1．（23-24高二下·广西南宁·阶段练习）已知点，，，，则异面直线与所成角的正弦值为（）A．B．C．D．2．（23-24高二上·广东深圳·期末）正方体中，M是中点，则异面直线CM与所成角的余弦值是（）A．B．C．D．3．（23-24高二下·江苏常州·期中）已知四棱锥的底面为直角梯形，，底面，且，，则异面直线与所成的角的余弦值为（）A．B．C．D．4．（23-24高二下·陕西榆林·开学考试）如图，在三棱锥中，为等边三角形，为等腰直角三角形，，平面平面，为的中点，则异面直线与所成角的余弦值为（）A．B．C．D．5．（23-24高二上·广东中山·期中）如图，圆锥的轴截面为等边三角形，为弧的中点，，分别为母线、的中点，则异面直线和所成角的大小为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．6．（23-24高二上·四川绵阳·期末）如图，已知菱形所在平面与矩形所在平面相互垂直，且，为线段的中点.则直线与的所成的角为（）A．B．C．D．②利用空间向量求线面角策略方法利用向量法求线面角的两种方法【题型精练】一、解答题1．（23-24高二下·上海·期末）如图，在三棱柱中，底面，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，，点，分别为与的中点．(1)证明：平面．(2)求与平面所成角的正弦值．2．（23-24高二下·山西·阶段练习）如图，在四棱锥中，平面底面，，，，，，．(1)求证：平面；(2)求直线与平面所成角的正弦值．3．（2024·河南·三模）如图，在直三棱柱中，是棱BC上一点（点D与点不重合），且，过作平面的垂线．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明：；(2)若，当三棱锥的体积最大时，求AC与平面所成角的正弦值．4．（23-24高二下·广东惠州·阶段练习）如图，已知为等腰梯形，点为以为直径的半圆弧的上一点，平面平面为的中点，．(1)求证：平面；(2)求直线与平面所成角的正弦值．5．（23-24高二下·河南濮阳·阶段练习）如图，在四棱锥中，正方形的边长为3，点，分别在棱，上（不含端点），，且，点在棱上，．(1)证明：；(2)若点到平面的距离为2，，求直线与平面所成角的大小．6．（23-24高二下·山西运城·期中）如图，四棱锥的底面是矩形，平面平面ABCD，M是棱PD上的动点，是棱AB上的一点，且.小学、初中、高中各种试卷真题知识归纳文案合...