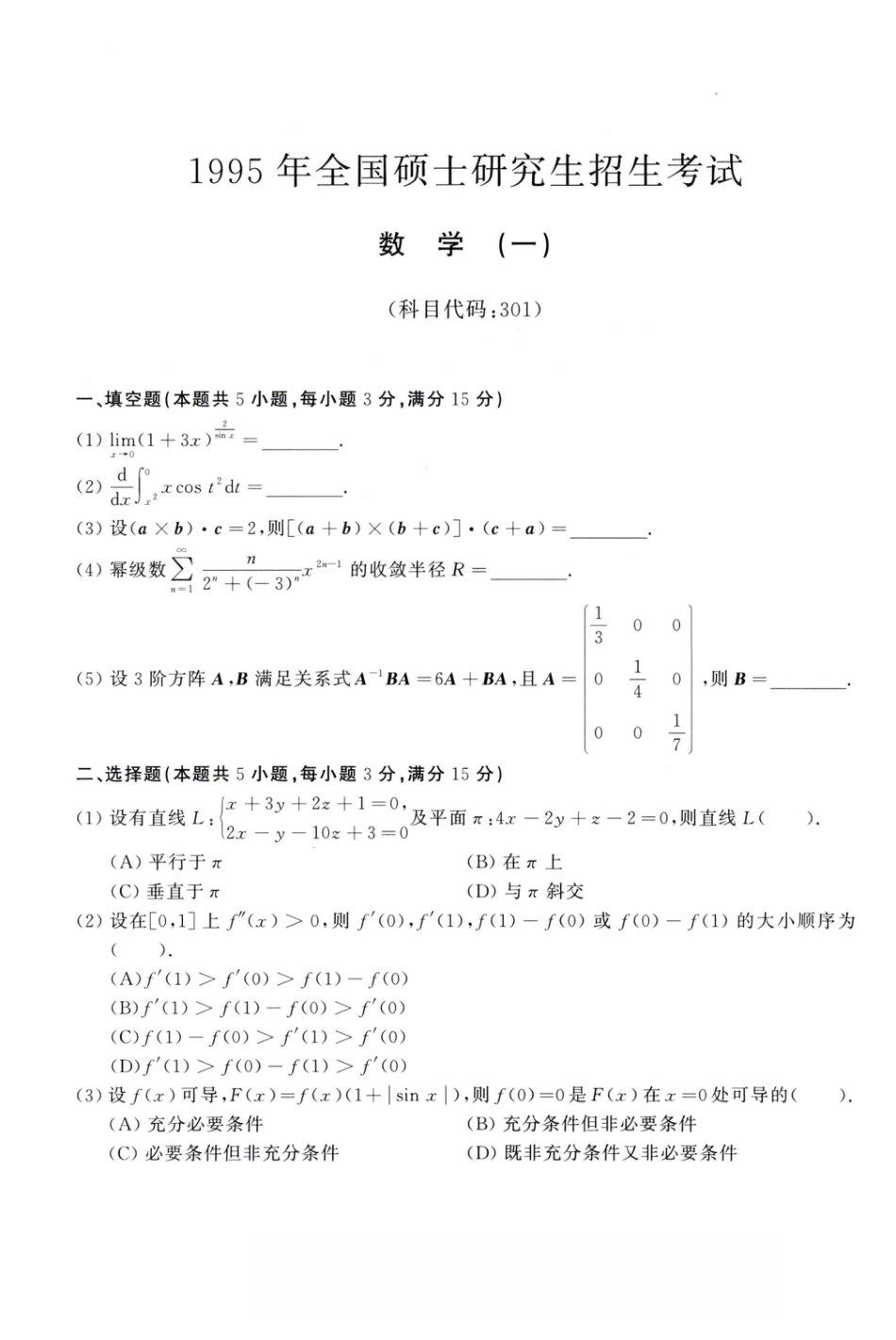
01995年全国硕士研究生招生考试数学(一)(科目代码：301)一、填空题(本题共5小题，每小题3分，满分15分)2(1)lim(l+3工)砧=.dr°(2)-—xcost2At=.cLcJ,-------------(3)设(aXb)•c=2?则［(a+b)X(b+c)］•(c+a)=________.(4)幕级数£…：。、”严的收敛半径R=________•T0(5)设3阶方阵满足关系式A^BA=6A+BA,且人=0丄400二、选择题(本题共5小题，每小题3分，满分15分)(1)设有直线L：］+'十十及平面兀：4鼻一2夕+z—2=0,则直线L().【2工一y一10z+3=0(A)平行于兀(E)在兀上(C)垂直于TT(D)与7T斜交(2)设在［0,叮上厂Q)>0,则/(0),/(1),/(1)-/(0)或/(0)-/(I)的大小顺序为().(A)/Z(l)>/(0)>f(l)-/(0)(B)y'(l)>/(l)-f(0)>/'(0)(C)f(1)-/(o)>/71)>/7o)(D)y'⑴>f(0)-/(l)>y'(0)(3)设_/(z)可导，F(z)—f(.x)(1+|sinx|),则/"(0)=0是F(z)在z=0处可导的().(A)充分必要条件(E)充分条件但非必要条件(C)必要条件但非充分条件(D)既非充分条件又非必要条件，则B=01_(4)设un=(—1)"ln(1+，则级数().(A)》“”与工都收敛n=1n=1oooo(C)工“”收敛而工诉发散n=\n=1(E)A%”与》“7都发散n=1n=1/Qiia12Q13、如1(5)设A二a21a22a23,B—a11a31a32a33a31+Q1100\P2=010，则必有().0J(D)工“”发散而工记收敛n=ln=la22a23\10a12a131,P1=100a32+Q12a33+a13'001(A)AP1P2=b(OP1P2A=B三、(本题共2小题，每小题5分，满分10分)(B)AP2P1=b(d)p2p1a=b(1)设“=fG,y,z),(p(jcz,ey,z)=0,y=sin工，其中于,卩都具有一阶连续的偏导数，且萨H0,求竟(2)设函数八工)在区间［0,1］上连续，并设\1fCx)dx=A,求「dr•Q)/'(y)dy.JoJoJx四、(本题共2小题，毎小题6分，满分12分)(1)计算曲面积分jpdS，其中工为锥面z=J工“+在柱体jcz+y22工内的部分.(2)将函数/(工)=工一1(0£工£2)展开成周期为4的余弦级数.五、（本题满分7分）设曲线L位于工0夕平面的第一象限内丄上任一点M处的切线与夕轴总相交，交点记为A.已知顾\=\OA且L过点,求L的方程.六、（本题满分8分）设函数QQ』）在工①平面上具有一阶连续偏导数，曲线积分J/Qdz+QCz,，）⑮与路径r(“i)r(i,t)无关，并且对任意/恒有|2pdz+Q(z,y)d；y=|2xydx+QQ,y)dy,求Q(z,y).J(0,0)J(0,0)七、（本题满分8分）设函数/（J7）,g（j：）在［a,b］上存在二阶导数，并且g"（z）H0,f（a）=f（b）=g（a）=g（b）=0,试证：（1）在开区间（a,b）内g（H）工0;（2）在开区间a,b）内至少存在一点w,使广票=厶黑.g（W）g（W）八、（本题满分7分）设3阶实对称矩阵A的特征值为心=—1,入2=入3=1，对应于入1的特征向量为§1=（0,1,1）T,求A.九、（本题满分6分）设A是九阶矩阵，满足AAt=E（E为n阶单位矩阵,为A的转置矩阵），|A|<0,求\A+E\.十、填空题（本题共2小题，每小题3分，满分6分）（1）设X表示10次独立重复射击命中目标的次数，每次射中目标的命中率为0.4,则X2的数学期望E（X2）=________.34（2）设x和y为两个随机变量，且p{x^o,y>0}=y,F{x>0}=p{y^o}=y,nijP{max（X，Y）0}=________・十一、（本题满分6分）仏一工g>0设随机变量X的概率密度为/xQ）='"，求随机变量Y=ex的概率密度fY（y\IO9工VO9