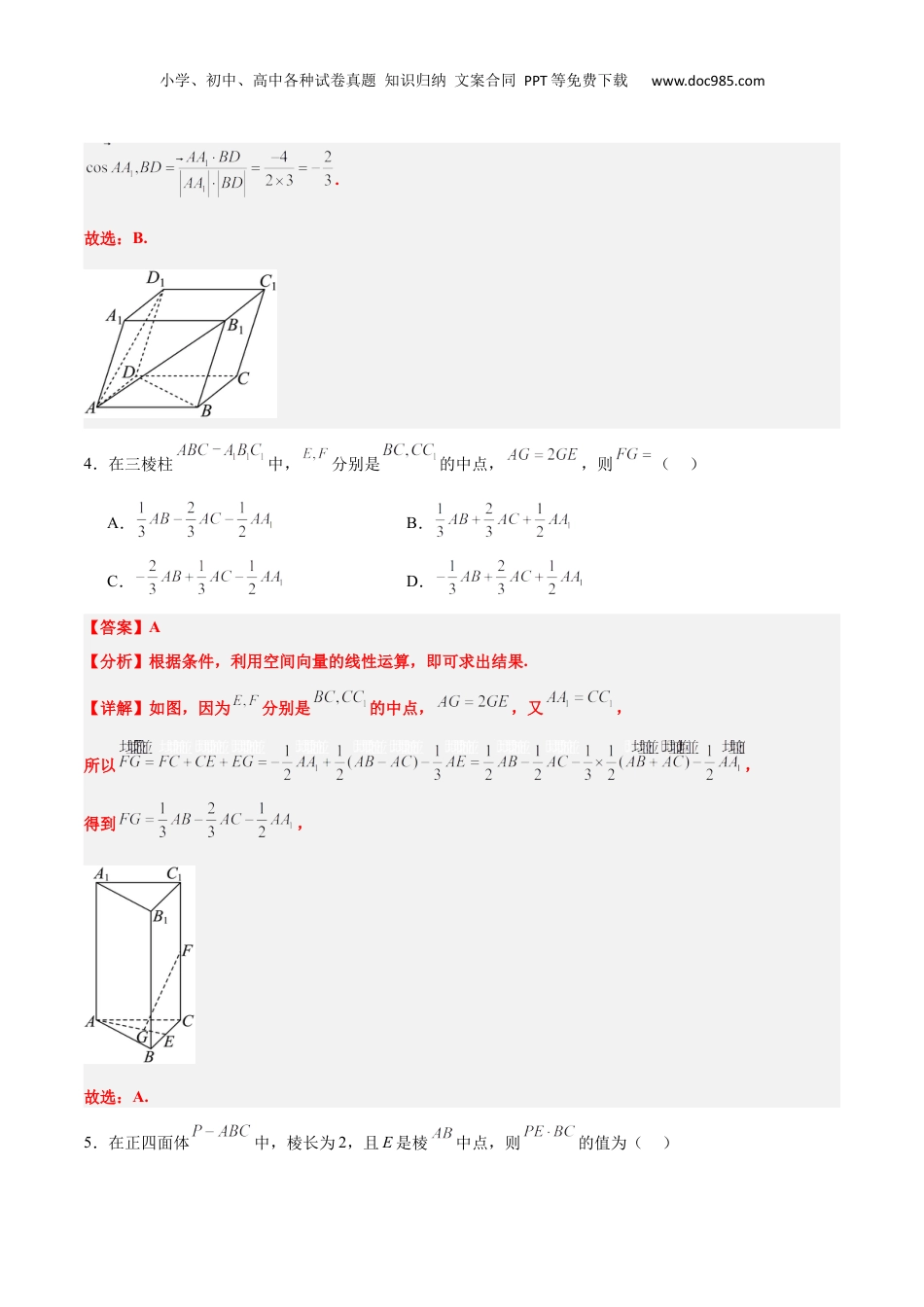
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第一章空间向量与立体几何综合检测（考试时间：120分钟试卷满分：150分）注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。第一部分（选择题共58分）一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。1．如图，在三棱柱中，（）A．B．C．D．【答案】D【分析】利用空间向量的线性运算计算即可.【详解】由题意可知：.故选：D2．已知向量，，，若，，三个向量共面，则实数，的取值小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com可能分别为（）A．，2B．2，2C．，1D．1，5【答案】D【分析】利用空间向量共面的条件，设实数，满足，列出方程组求解即可.【详解】因为三向量共面，所以存在实数，使得，所以，解得，故当时满足条件.故选：D.3．已知平行六面体中，，，，则（）A．B．C．D．【答案】B【分析】利用向量的线性运算法则和数量积的性质化简条件可求，结合向量夹角公式可求结论.【详解】因为所以，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com.故选：B.4．在三棱柱中，分别是的中点，，则（）A．B．C．D．【答案】A【分析】根据条件，利用空间向量的线性运算，即可求出结果.【详解】如图，因为分别是的中点，，又，所以，得到，故选：A.5．在正四面体中，棱长为2，且E是棱中点，则的值为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】A【分析】在正四面体中，根据向量的数量积的运算，即可求解【详解】如图所示，由正四面体的性质可得，，由E是棱中点，，故选：A．6．在正四面体中，分别为的中点，则异面直线所成角的正切值为（）A．B．C．D．【答案】D【分析】根据向量基本定理表示向量，结合向量的数量积公式计算夹角余弦值，从而可得正切值.【详解】设正四面体棱长为1，设，，，则，，∴，，. 分别为的中点，，是等边三角形，∴，，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com．设异面直线所成角为，则则，所以，所以异面直线所成角的正切值为.故选：D.7．在正方体中，点在线段上，且.当为锐角时，则实数的取值范围为（）A．B．C．D．【答案】C【分析】建立空间直角坐标系，将为锐角转化为，利用向量的坐标运算求解即可.【详解】如图建立空间直角坐标系，设正方体的棱长为，则，则，所以，所以，，由图可知，，所以为锐角等价于，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以又，解得.故选：C.8．如图，在体积为5的多面体ABCDPQ中，底面ABCD是平行四边形，为BC的中点，.则平面PCD与平面QAB夹角的余弦值为（）A．B．C．D．【答案】C【分析】先证明，再根据体积公式，结合棱柱与棱锥的体积关系，结合等体积法可得，即可建立空间直角坐标系，运用法向量求解.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【详解】在中，由余弦定理可得，所以，所以，所以．又因为，平面,所以平面,平面，所以．由于,所以四边形为平行四边形，所以．又，所以，所以．因为，所以，又，平面，所以平面，则面．取中点，连接，由面，面，则面面，面面，根据已知易知，所以为三棱柱，设，多面体的体积为，则．解得．建立如图所示的空间直角坐标系，则，．则平面的一个法向量，且，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com设平面的一个法向量，则即取．所以，平面与平面夹角的余弦值为．故选：C二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9．已知空间...