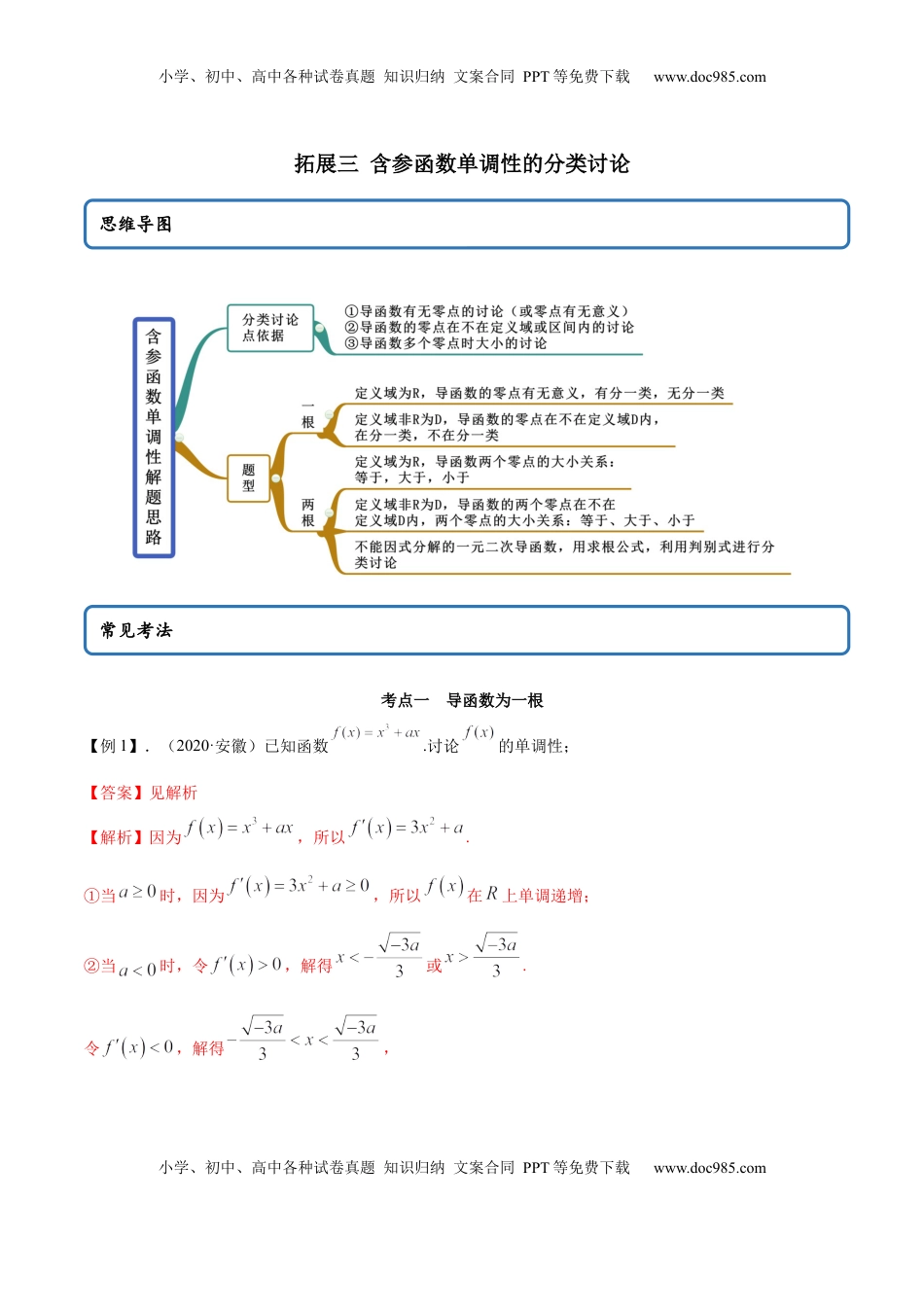
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com拓展三含参函数单调性的分类讨论考点一导函数为一根【例1】．（2020·安徽）已知函数.讨论的单调性；【答案】见解析【解析】因为，所以.①当时，因为，所以在上单调递增；②当时，令，解得或.令，解得，思维导图常见考法小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则在，上单调递增；在上单调递减.【一隅三反】1．（2020·河南）已知函数.讨论函数的单调性；【答案】答案见解析【解析】的定义域为，，当时，，则在上是增函数；当时，，所以；或；，所以在上是减函数，在和上是增函数.2．（2020·山西运城）已知函数.讨论的单调性；【答案】具体见解析【解析】函数，定义域为，，当时，.故在定义域上单调递增，此时无减区间.当时，令，得；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com当时，，故单调递增；当时，，故单调递减.综上所述，当时，在定义域上单调递增，此时无减区间；当时，在上单调递增，在上单调递减.3．（2020·青海高二期末（理））已知函数，.讨论的单调性；【答案】当时，在上单调递减；当时，在上单调递减，在上单调递增；【解析】因为，所以.当时，恒成立，在上单调递减；当时，由，得；由，得.故在上单调递减，在上单调递增.综上，当时，在上单调递减；当时，在上单调递减，在上单调递增.考点二导函数为两根小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例2】．（2020·四川南充·高二期末（理））已知函数，.（1）讨论的单调性；（2）若对任意，都有成立，求实数的取值范围.【答案】（1）当时，在上，是减函数,当时，在上，是减函数,在上，是增函数；【解析】解：函数f（x）的定义域为（0，+∞）又当a≤0时，在（0，+∞）上，f′（x）＜0，f（x）是减函数当a＞0时，由f′（x）=0得：或（舍）所以：在上，f′（x）＜0，f（x）是减函数在上，f′（x）＞0，f（x）是增函数【一隅三反】1．（2020·赣州市赣县第三中学高二月考（文））已知函数，函数．判断函数的单调性；【答案】答案见解析小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解析】由题意得，；∴．当时，，函数在上单调递增；当时，令，有：在上单调递增；令，有：在上单调递减；综上，当时，函数在上单调递增；当时，函数在上单调递增，在上单调递减．2．（2020·河南郑州）已知函讨论的单调性；（2）若有两个零点，求的取值范围.【答案】答案见解析【解析】.当时，令，得，令，得.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com故在单调递减，在单调递增.当时，令，得，.①当即时，，在R上单调递增.②当即时，在上单调递减，在，上单调递增.③当即时，在上单调递减，在，上单调递增.3．已知函数，讨论函数的单调性；【答案】见解析【解析】因为，所以.令，解得或.若，当即或时，故函数的单调递增区间为；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com当即时，故函数的单调递减区间为.若，则，当且仅当时取等号，故函数在上是增函数.若，当即或时，故函数的单调递增区间为；当即时，故函数的单调递减区间为.综上，时，函数单调递增区间为，单调递减区间为；时，函数单调递增区间为；时，函数单调递增区间为，单调递减区间为.考点三不能因式分解【例3】．（2019·全国湖北·高二期中（文））设函数讨论...