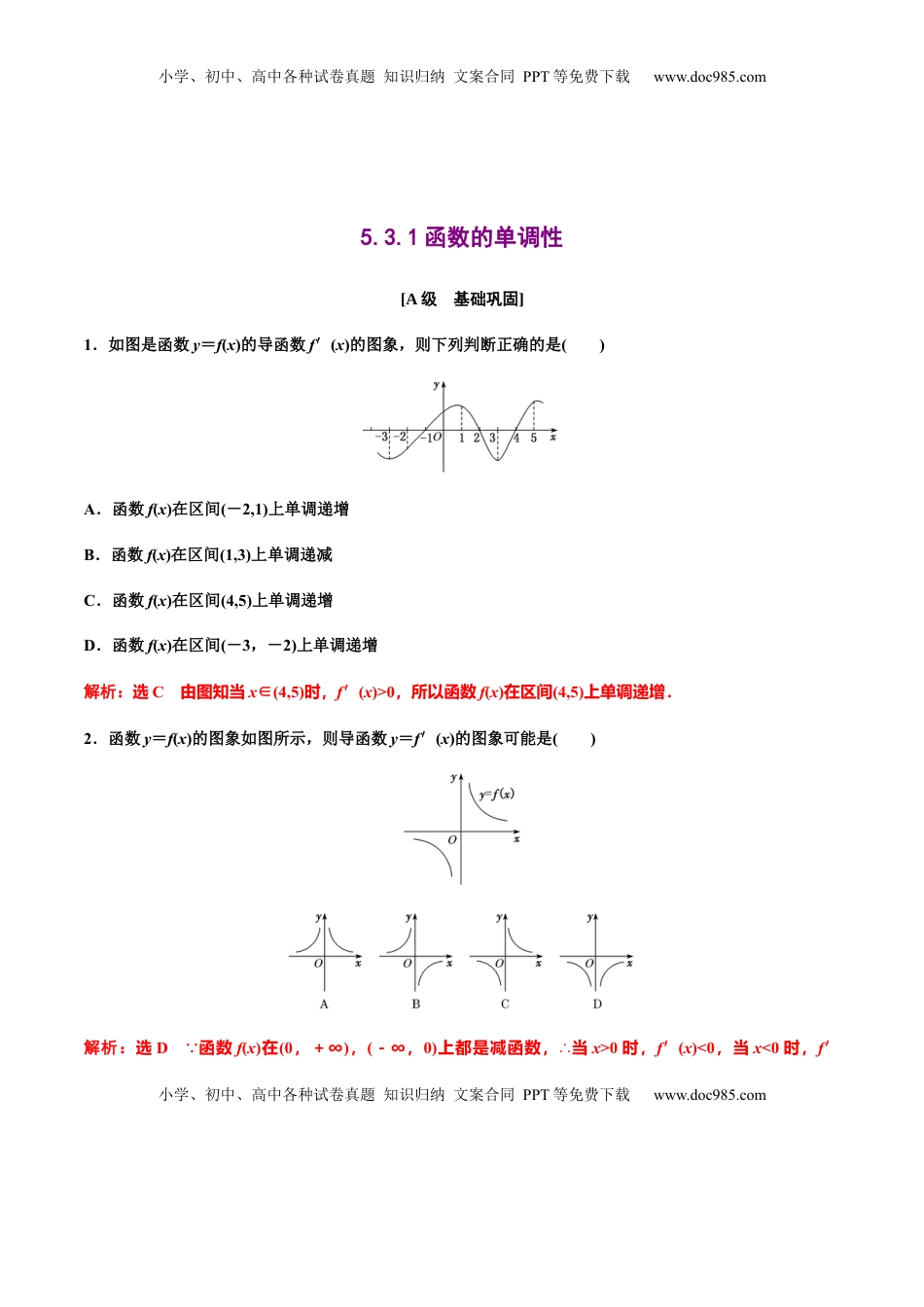
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5.3.1函数的单调性[A级基础巩固]1．如图是函数y＝f(x)的导函数f′(x)的图象，则下列判断正确的是()A．函数f(x)在区间(－2,1)上单调递增B．函数f(x)在区间(1,3)上单调递减C．函数f(x)在区间(4,5)上单调递增D．函数f(x)在区间(－3，－2)上单调递增解析：选C由图知当x∈(4,5)时，f′(x)>0，所以函数f(x)在区间(4,5)上单调递增．2．函数y＝f(x)的图象如图所示，则导函数y＝f′(x)的图象可能是()解析：选D 函数f(x)在(0，＋∞)，(－∞，0)上都是减函数，∴当x>0时，f′(x)<0，当x<0时，f′小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(x)<0，故选D.3．函数f(x)＝x2－lnx的单调递减区间为()A．(0,1)B．(0,1)∪(－∞，－1)C．(－∞，1)D．(－∞，＋∞)解析：选A y＝x2－lnx的定义域为(0，＋∞)，∴y′＝x－，令y′<0，即x－<0，解得0<x<1.故选A.4．下列函数中，在(0，＋∞)内为增函数的是()A．y＝sinxB．y＝xexC．y＝x3－xD．y＝lnx－x解析：选BB项中，y＝xex，y′＝ex＋xex＝ex(1＋x)，当x∈(0，＋∞)时，y′>0，∴y＝xex在(0，＋∞)内为增函数．5．若f(x)＝，e<a<b，则()A．f(a)>f(b)B．f(a)＝f(b)C．f(a)<f(b)D．f(a)f(b)>1解析：选A由f′(x)＝<0，解得x>e，∴f(x)在(e，＋∞)上为减函数， e<a<b，∴f(a)>f(b)．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com6．已知函数f(x)＝kex－1－x＋x2(k为常数)，曲线y＝f(x)在点(0，f(0))处的切线与x轴平行，则f(x)的单调递减区间为________．解析：f′(x)＝kex－1－1＋x. 曲线y＝f(x)在点(0，f(0))处的切线与x轴平行，∴f′(0)＝k·e－1－1＝0，解得k＝e，故f′(x)＝ex＋x－1.令f′(x)<0，解得x<0，故f(x)的单调递减区间为(－∞，0)．答案：(－∞，0)7．已知函数f(x)＝x3－ax－1，若f(x)在(－1,1)上单调递减，则a的取值范围为________．解析： f(x)＝x3－ax－1，∴f′(x)＝3x2－a.要使f(x)在(－1,1)上单调递减，则f′(x)≤0在x∈(－1,1)上恒成立，则3x2－a≤0，故a≥3x2在x∈(－1,1)上恒成立，在x∈(－1,1)上，3x2<3，即a≥3，∴a的取值范围为[3，＋∞)．答案：[3，＋∞)8．如图为函数f(x)的图象，f′(x)为函数f(x)的导函数，则不等式<0的解集为________．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com解析：由题图知，当x∈(－∞，－3)∪(－1,1)时，f′(x)<0，当x∈(－3，－1)∪(1，＋∞)时，f′(x)>0，故不等式<0的解集为(－3，－1)∪(0,1)．答案：(－3，－1)∪(0,1)9．已知函数f(x)＝2ax－，x∈(0,1]．若f(x)在(0,1]上是增函数，求a的取值范围．解：由已知，得f′(x)＝2a＋. f(x)在(0,1]上单调递增，∴f′(x)≥0，即a≥－在(0,1]上恒成立．而g(x)＝－在(0,1]上是增函数，∴g(x)max＝g(1)＝－1，∴a≥－1.当a＝－1时，f′(x)＝－2＋，对x∈(0,1]有f′(x)≥0，∴当a＝－1时，f(x)在(0,1]上是增函数．综上，若f(x)在(0,1]上为增函数，a的取值范围是[－1，＋∞)．10．已知二次函数h(x)＝ax2＋bx＋2，其导函数y＝h′(x)的图象如图，f(x)＝6lnx＋h(x)．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)求函数f(x)的解析式；(2)若函数f(x)在区间上是单调函数，求实数m的取值范围．解：(1)由已知，h′(x)＝2ax＋b，其图象为直线，且过(0，－8)，(4,0)两点，把两点坐标代入h′(x)＝2ax＋b，解得∴h(x)＝x2－8x＋2，h′(x)＝2x－8，∴f(x)＝6lnx＋x2－8x＋2.(2) f′(x)＝＋2x－8＝(x>0)．∴当x变化时，f′(x)，f(x)的变化情况如下表：x(0,1)1(1,3)3(3，＋∞)f′(x)...