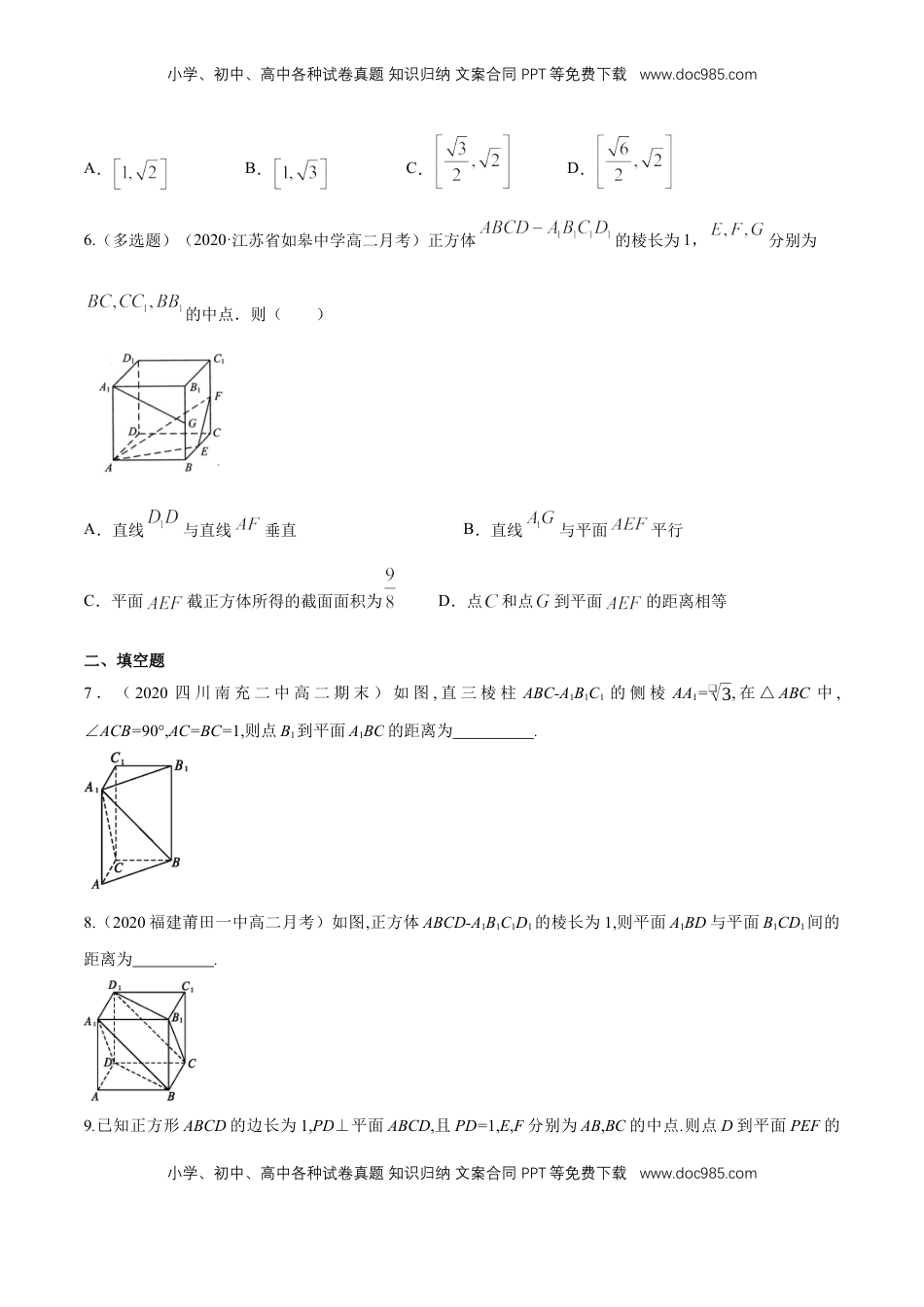
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1.4.2用空间向量研究距离、夹角问题(1)-B提高练一、选择题1．（2020安徽安庆高二期中）若点A（2，3，2）关于xoz平面的对称点为A'，点B（﹣2，1，4）关于y轴对称点为B'，点M为线段A'B'的中点，则|MA|＝（）A．B．C．5D．2．（2020四川广安高二校级月考）已知直线l的方向向量为＝（﹣1，0，1），点A（1，2，﹣1）在l上，则点P（2，﹣1，2）到l的距离为（）A．B．4C．D．33.如图,已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,且GC=2,则点B到平面EFG的距离为()A.❑√1010B.2❑√1111C.35D.14．（2020山东菏泽三中高二期末）在棱长为a的正方体ABCD﹣A1B1C1D1中，M是AA1的中点，则点A到平面MBD的距离是（）A．aB．aC．aD．a5．（2020·湖南高二（理））正方体的棱长为1，动点在线段上，动点在平面A1B1C1D1上，且平面.线段长度的取值范围为()小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．6.（多选题）（2020·江苏省如皋中学高二月考）正方体的棱长为1，分别为的中点．则（）A．直线与直线垂直B．直线与平面平行C．平面截正方体所得的截面面积为D．点和点到平面的距离相等二、填空题7．（2020四川南充二中高二期末）如图,直三棱柱ABC-A1B1C1的侧棱AA1=❑√3,在△ABC中,∠ACB=90°,AC=BC=1,则点B1到平面A1BC的距离为.8.（2020福建莆田一中高二月考）如图,正方体ABCD-A1B1C1D1的棱长为1,则平面A1BD与平面B1CD1间的距离为.9.已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,E,F分别为AB,BC的中点.则点D到平面PEF的小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com距离为，直线AC到平面PEF的距离.10．（2020湖南师大附中高二期中）已知三棱锥S﹣ABC，满足SA，SB，SC两两垂直，且SA＝SB＝SC＝2，Q是三棱锥S﹣ABC外接球上一动点，则点Q到平面ABC的距离的最大值为.三、解答题11.（2020银川一中高二月考）如图所示,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=❑√2,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,问:线段AD上是否存在一点Q,使得它到平面PCD的距离为❑√32?若存在,求出AQQD的值;若不存在,说明理由.12．（2020四川广元二中高二月考）已知Rt△ABC如图（1），∠C＝90°，D．E分别是AC，AB的中点，将△ADE沿DE折起到PDE位置（即A点到P点位置）如图（2）使∠PDC＝60°．（I）求证：BC⊥PC；（Ⅱ）若BC＝2CD＝4，求点D到平面PBE的距离．