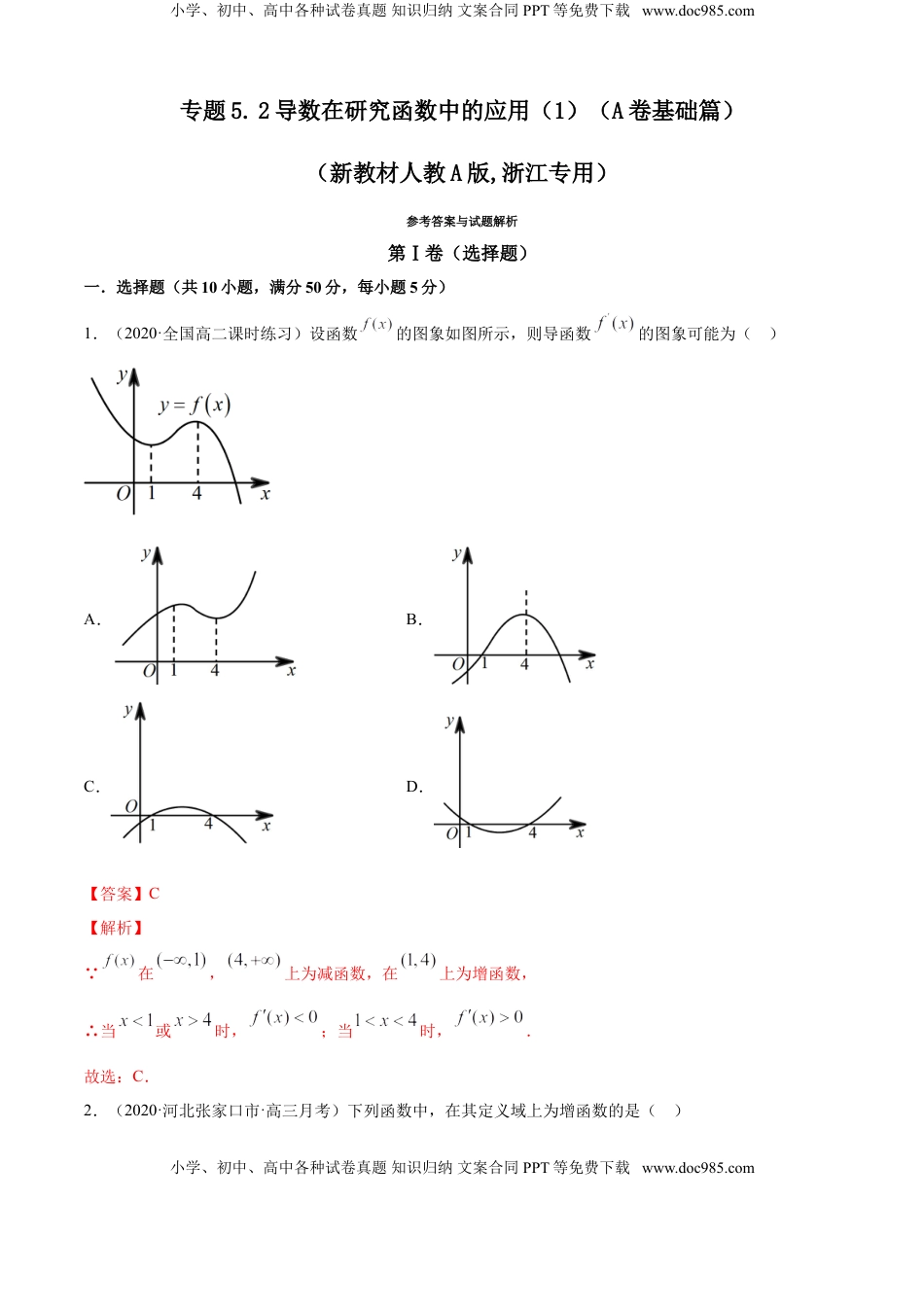
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题5.2导数在研究函数中的应用（1）（A卷基础篇）（新教材人教A版,浙江专用）参考答案与试题解析第Ⅰ卷（选择题）一．选择题（共10小题，满分50分，每小题5分）1．（2020·全国高二课时练习）设函数的图象如图所示，则导函数的图象可能为（）A．B．C．D．【答案】C【解析】 在，上为减函数，在上为增函数，∴当或时，；当时，．故选：C．2．（2020·河北张家口市·高三月考）下列函数中，在其定义域上为增函数的是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】C【解析】对于A选项，函数为偶函数，在上递增，在上递减；对于B选项，函数在上递减；对于C选项，在上恒成立，则函数在其定义域上递增；对于D选项，函数在上递减.故选：C．3．（2020·赣州市赣县第三中学高三期中（文））已知函数，则其单调增区间是（）A．B．C．D．【答案】A【解析】由，函数定义域为，求导，令，得或（舍去）所以单调增区间是故选：A.4．（2020·张家界市民族中学高二月考）函数的单调递增区间为（）A．B．C．D．【答案】C【解析】小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，由得，即，所以函数的单调递增区间为.故选：C5．（2020·全国高三专题练习）如图所示为的图象，则函数的单调递减区间是（）A．B．C．D．【答案】C【解析】由导函数图象，知或时，，∴的减区间是，．故选：C．6．（2019·江西九江市·高二期末（理））函数的递增区间是（）A．B．和C．D．和【答案】C【解析】小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com因为的定义域为，，由，得，解得，所以的递增区间为.故选：C.7．（2020·四川内江市·高三三模（文））函数的图像大致为（）A．B．C．D．【答案】C【解析】，当时，，当时，，所以函数在上单调递增，在上单调递减.故选：C8．（2020·广东深圳市·高三开学考试）已知函数与的图象如图所示，则不等式组解集为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】B【解析】由导函数与原函数单调性关系知图中实线是的图象，虚线是的图象，不等式组解集是．故选：B．9．（2020·全国高三专题练习）已知是定义在上的函数的导函数，且满足对任意的都成立，则下列选项中一定正确的是（）A．B．C．D．【答案】D【解析】令，则，故为上的增函数，所以即，故选：D.10．（2020·黄梅国际育才高级中学高二期中）已知函数在内不是单调函数，则实数的取值范围是（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】A【解析】 ，在内不是单调函数，故在存在变号零点，即在存在零点，∴.故选：A.第Ⅱ卷（非选择题）二．填空题（共7小题，单空每小题4分，两空每小题6分，共36分）11．（2020·长顺县文博高级中学有限公司高三月考）函数的单调减区间是__________.【答案】【解析】，令，解得，所以函数的单调减区间为.故答案为：12．（2020·全国高三专题练习）函数的单调递减区间是______．【答案】【解析】的定义域是，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com令，解得：，所以在递减，故答案为13．（2019·全国高三月考（文））已知，函数在上是单调增函数，则的最大值是_______．【答案】6【解析】，令，得或，所以，解得．故答案为：614．（2018·全国高二专题练习）函数在区间______上是增函数，在...