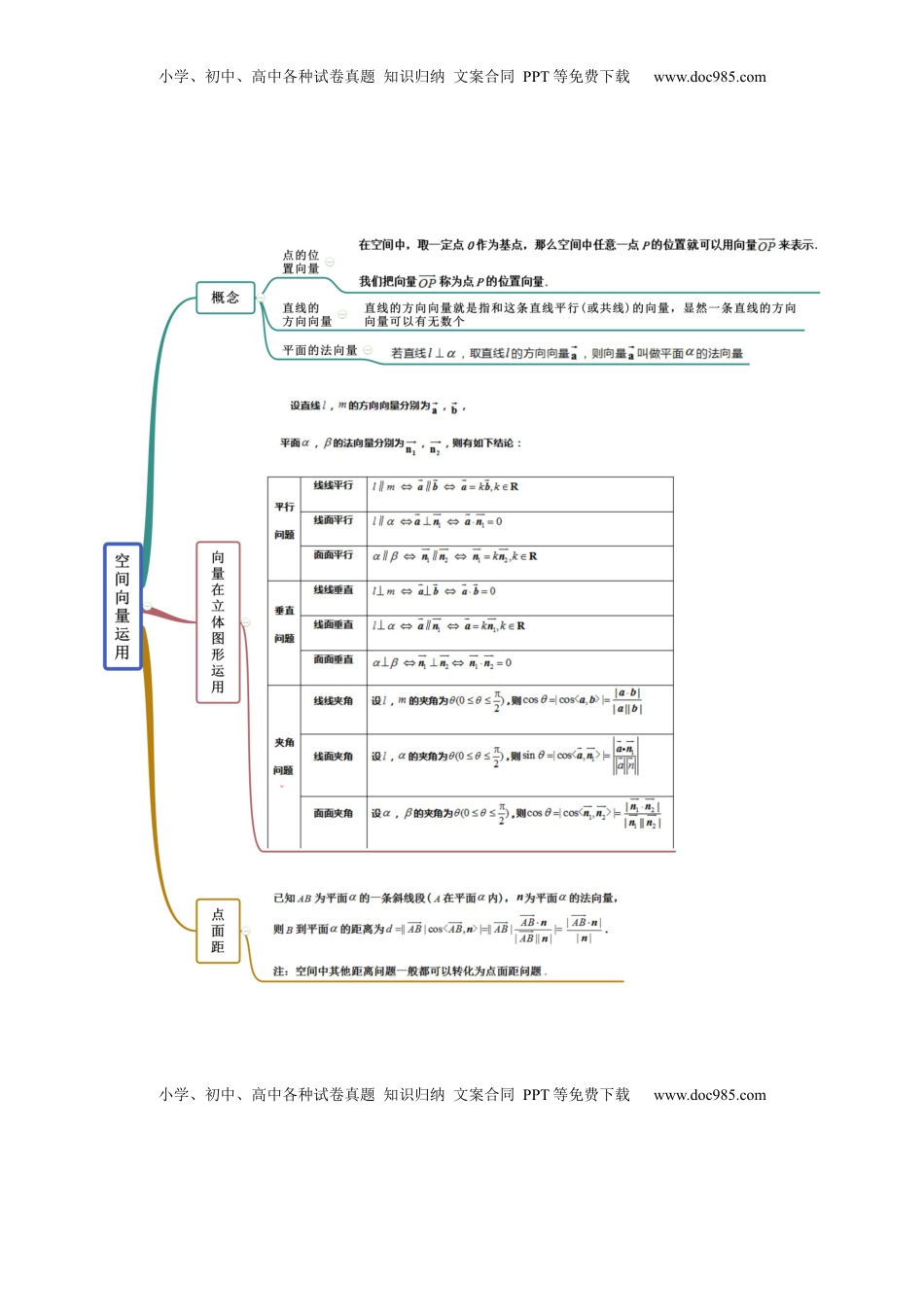
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1.4.2空间向量应用（二）思维导图小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com考点一空间向量求线线角【例1】（2020·全国高三一模（文））如图，四棱锥中，底面是矩形，，，，，是等腰三角形，点是棱的中点，则异面直线与所成角的余弦值是（）常见考法小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【一隅三反】1．（2020·河南高二）已知在正方体中，P为线段上的动点，则直线与直线所成角余弦值的范围是（）向量法求异面直线所成角的一般步骤(1)选择三条两两垂直的直线建立空间直角坐标系；(2)确定异面直线上两个点的坐标，从而确定异面直线的方向向量；(3)利用向量的夹角公式求出向量夹角的余弦值；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．2.三棱柱ABC－A1B1C1中，△ABC为等边三角形，AA1⊥平面ABC，AA1＝AB，N，M分别是A1B1，A1C1的中点，则AM与BN所成角的余弦值为()A.B.C.D.3．已知四棱锥SABCD的底面是正方形且侧棱长与底面边长都相等，E是SB的中点，则AE，SD所成的角的余弦值为()A．B．C．D．考点二空间向量求线面角【例2】（2020·全国高二）如图所示，是四棱锥的高，四边形为正方形，点是线段的中点，.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）求证：；（2）若点是线段上靠近的四等分点，求直线与平面所成角的正弦值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一隅三反】1．（2020·浙江高三开学考试）如图，四棱锥中，，，，，，．（1）求证：；（2）求直线与平面所成角的正弦值．若直线l与平面α的夹角为θ，直线l的方向向量l与平面α的法向量n的夹角为β，则θ＝－β或θ＝β－，故有sinθ＝|cosβ|＝.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．（2020·天津河西.高三二模）在正四棱柱中，，为的中点.（1）求证：平面；（2）求证：平面；（3）若为上的动点，使直线与平面所成角的正弦值是，求的长.3．（2020·江苏）如图，在三棱锥P-ABC中，AC⊥BC，且，AC=BC=2，D，E分别为AB，PB中点，PD⊥平面ABC，PD=3.(1)求直线CE与直线PA夹角的余弦值；(2)求直线PC与平面DEC夹角的正弦值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com考点三空间向量求二面角【例3】（2020·河南高三其他（理））如图，在三棱锥中，．（1）证明：平面；（2）求二面角的余弦值．【一隅三反】1．（2020·全国）如图，圆的直径，为圆周上不与点、重合的点，垂直于圆所在平面，利用向量法求二面角的大小的关键是确定平面的法向量，求法向量的方法主要有两种：①求平面的垂线的方向向量；②利用法向量与平面内两个不共线向量的数量积为零，列方程组求解小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，.（1）求证：平面；（2）求二面角的余弦值.2．（2020·全国）如图，已知四棱锥中，是平行四...