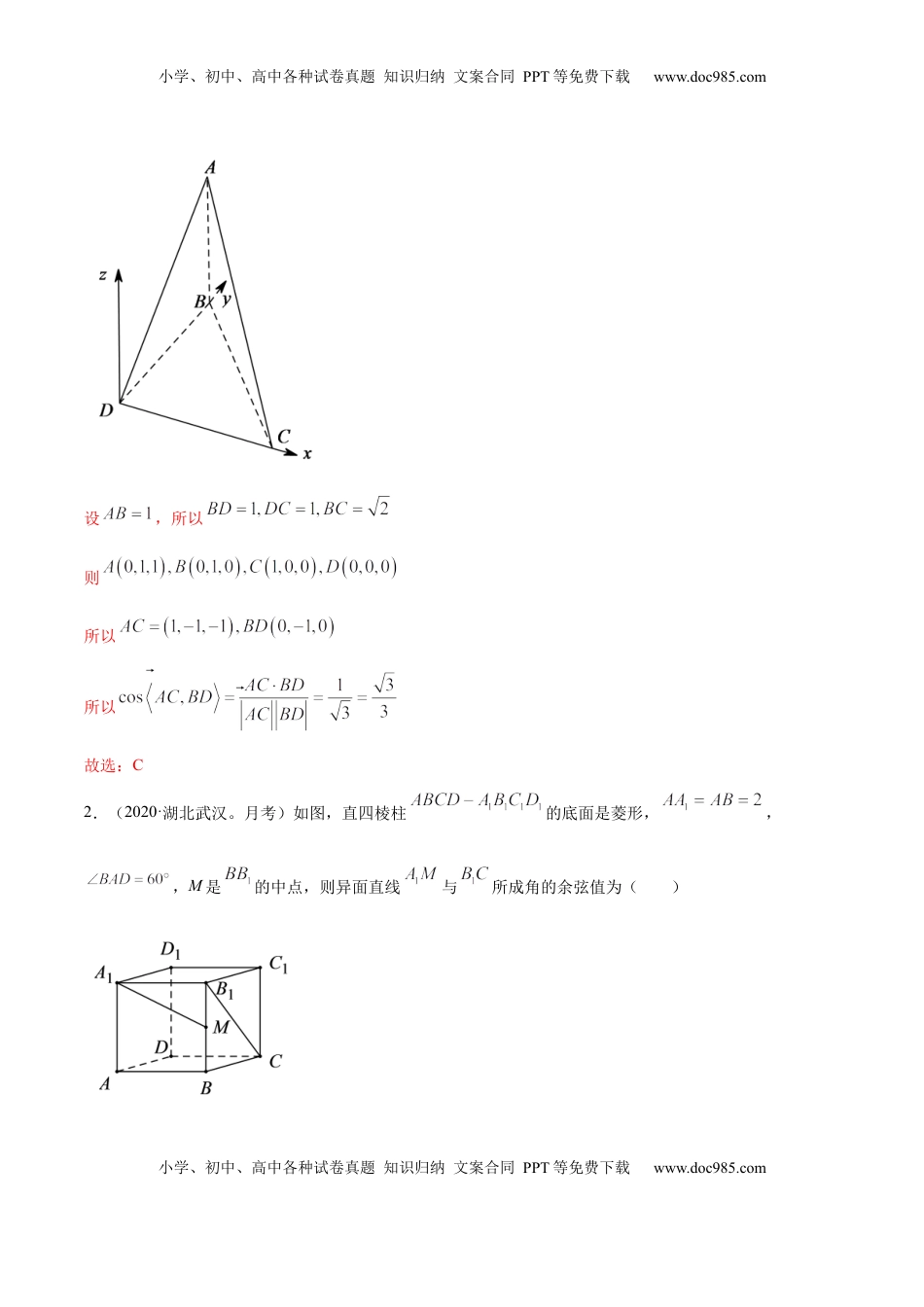
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1.4.2空间向量应用（二）【题组一空间向量求线线角】1．（2020·宜昌天问教育集团高二期末）如图，将两个全等等腰直角三角形拼成一个平行四边形，将平行四边形沿对角线折起，使平面平面，则直线与所成角余弦值为（）A．B．C．D．【答案】C【解析】由平面平面，平面平面，平面所以平面，又平面所以，又所以作轴//,建立空间直角坐标系如图小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com设，所以则所以所以故选：C2．（2020·湖北武汉。月考）如图，直四棱柱的底面是菱形，，，M是的中点，则异面直线与所成角的余弦值为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】D【解析】由题意可得，故选：D3．（2019·绍兴鲁迅中学高二期中）如图，长方体中，，，、、分别是、、的中点，则异面直线与所成角的余弦值是（）A．0B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】A【解析】如图所以所以异面直线与所成角的余弦值故选：A4．（2019·浙江湖州.高二期中）在正方体中，异面直线与所成的角为（）A．B．C．D．【答案】D【解析】以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，设正方体ABCD﹣A1B1C1D1中棱长为1，则A（1，0，0），C（0，1，0），D（0，0，0），B1（1，1，1），＝（﹣1，1，0），＝（﹣1，﹣1，﹣1），小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com设异面直线AC与B1D所成的角为θ，则cosθ＝＝0，∴θ＝.∴异面直线AC与B1D所成的角为.故选：D.5．（2020·武汉外国语学校高一月考）如图，正三棱锥的侧棱长为3，底面边长为2，则与所成角的余弦值为______.【答案】【解析】设与的夹角为，则与的夹角也是小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则与所成角的余弦值为故答案为：【题组二空间向量求线面角】1．（2020·江苏高二）如图，在三棱锥P-ABC中，AC⊥BC，且，AC=BC=2，D，E分别为AB，PB中点，PD⊥平面ABC，PD=3.(1)求直线CE与直线PA夹角的余弦值；(2)求直线PC与平面DEC夹角的正弦值.【答案】(1)；(2).【解析】建立如图所示的空间直角坐标系，易知C(0，0，0)，A(2，0，0)，D(1，1，0)，E(，，)，P(1，1，3)，设直线CE与直线PA夹角为，则小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com整理得；直线CE与直线PA夹角的余弦值；(2)设直线PC与平面DEC夹角为，设平面DEC的法向量为，因为，所以有取，解得，，即面DEC的一个法向量为，，.直线PC与平面DEC夹角的正弦值为.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．（2020·沙坪坝.重庆八中）如图，四棱台中，底面是菱形，底面，且60°，，是棱的中点.（1）求证：；（2）求直线与平面所成线面角的正弦值.【答案】（1）证明见解析；（2）.【解析】（1）因为底面，所以因为底面是菱形，所以又，所以平面又由四棱台知，，，，四点共面小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以（2）如图，设交于点，依题意，且，，且，又由已知底面，得底面．以为原点，、、所在...