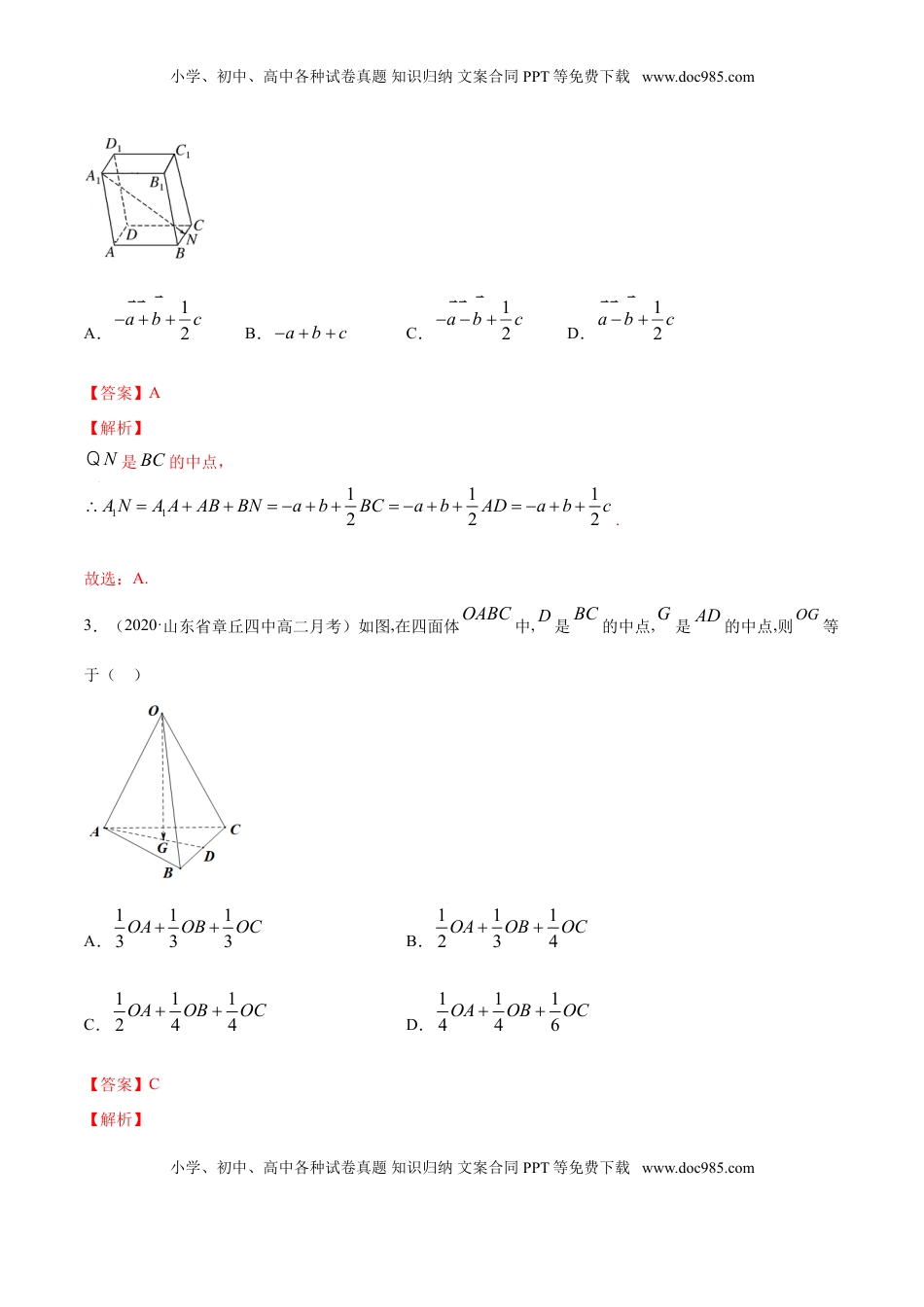
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题01空间向量及其运算、空间向量基本定理一、单选题1．（2019·全国高二课时练习）已知a，b，c是不共面的三个向量，则能构成一个基底的一组向量是（）A．2a，a﹣b，a+2bB．2b，b﹣a，b+2aC．a，2b，b﹣cD．c，a+c，a﹣c【答案】C【解析】对于A，因为2a=43（a﹣b）+23（a+2b），得2a、a﹣b、a+2b三个向量共面，故它们不能构成一个基底，A不正确；对于B，因为2b=43（b﹣a）+23（b+2a），得2b、b﹣a、b+2a三个向量共面，故它们不能构成一个基底，B不正确；对于C，因为找不到实数λ、μ，使a=λ•2b+μ（b﹣c）成立，故a、2b、b﹣c三个向量不共面，它们能构成一个基底，C正确；对于D，因为c=12（a+c）﹣12（a﹣c），得c、a+c、a﹣c三个向量共面，故它们不能构成一个基底，D不正确故选：C．2．（2020·贵州省铜仁第一中学高二开学考试）如图所示，在平行六面体1111ABCDABCD中，设1AAa��，ABb��，ADc��，N是BC的中点，试用a�，b�，c�表示1AN�（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．12abc���B．abc���C．12abc���D．12abc���【答案】A【解析】NQ是BC的中点，11111222ANAAABBNabBCabADabc.故选：A.3．（2020·山东省章丘四中高二月考）如图,在四面体OABC中,D是BC的中点,G是AD的中点,则OG等于（）A．111333OAOBOCB．111234OAOBOCC．111244OAOBOCD．111446OAOBOC【答案】C【解析】小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com在四面体OABC中,D是BC的中点,G是AD的中点12OGOAAD11()22OAABAC1()4OAOBOAOCOA111244OAOBOC故选:C.4．（2020·河南省高二期末）如图在平行六面体1111ABCDABCD中，E为11AD的中点，设ABa，ADb，1AAc，则CE（）A．12abcB．12abcC．12abcD．12abc【答案】A【解析】由题意结合平行六面体的性质可得1111CECCCDDE111111111222CCCDDAAAABADabc.故选：A.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．（2020·广东省红岭中学高二期末）AB�与CD�共线是直线AB∥CD的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】B【解析】根据向量共线的定义，可知若AB�与CD�共线，则它们所在的直线可能平行，也可能重合；若AB∥CD，则AB�与CD�共线；根据充分条件和必要条件的概念，可知AB�与CD�共线是直线AB∥CD的必要不充分条件，故选B点睛：向量共线的定义：如果表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫做共线向量或平行向量.6．（2020·广东省红岭中学高二期末）O为空间任意一点,,,ABC三点不共线,若OP�=111326OAOBOC�,则,,,ABCP四点A．一定不共面B．不一定共面C．一定共面D．无法判断【答案】C【解析】：点P在平面ABC内，O是平面ABC外的任意一点，则OPxOAyOBzOC�且1xyz．利用此推论可直接证明一定共面．详解：因为OP�=111326OAOBOC�，且1111326，所以,,,ABCP四点共面.7．（2019·随州市第一中学高二期中）空间ABCD、、、四点共面，但任意三点不共线，若P为该平面小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com外一点且5133PAPBxPCPD，则...