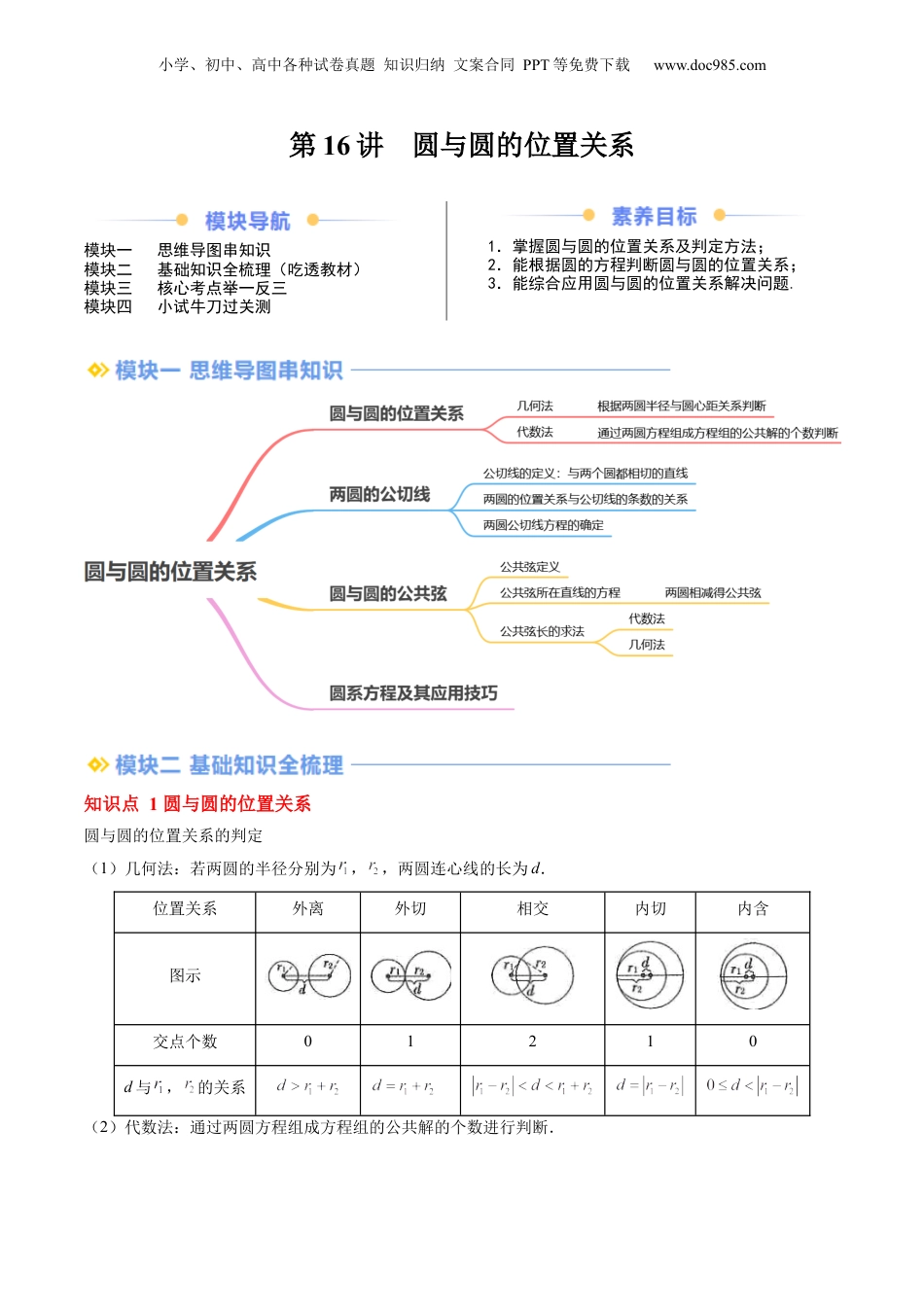
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第16讲圆与圆的位置关系模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．掌握圆与圆的位置关系及判定方法；2．能根据圆的方程判断圆与圆的位置关系；3．能综合应用圆与圆的位置关系解决问题.知识点1圆与圆的位置关系圆与圆的位置关系的判定（1）几何法：若两圆的半径分别为，，两圆连心线的长为d．位置关系外离外切相交内切内含图示交点个数01210d与，的关系（2）代数法：通过两圆方程组成方程组的公共解的个数进行判断．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com消元，一元二次方程知识点2两圆的公切线1、公切线的定义：与两个圆都相切的直线叫做两圆的公切线，包括外公切线和内公切线．2、两圆的位置关系与公切线的条数的关系位置关系外离外切相交内切内含图示公切线条数4条3条2条1条无公切线3、两圆公切线方程的确定（1）当公切线的斜率存在时，可设公切线方程为，由公切线的意义（两圆公公的切线）可知，两圆心到直线的距离分别等于两圆的半径，这样得到关于和的方程，解这个方程组得到，的值，即可写出公切线的方程；（2）当公切线的斜率不存在时，要注意运用数形结合的方法，观察并写出公切线的方程．知识点3圆与圆的公共弦1、公共弦的定义：圆与圆相交得到两个交点，这两点之间的线段就是两圆的公共弦．2、公共弦所在直线的方程圆：，圆：，则为两相交圆公共弦方程.【注意】（1）若与相切，则表示其中一条公切线方程；（2）若与相离，则表示连心线的中垂线方程.3、公共弦长的求法（1）代数法：将两圆的方程联立，解出两交点坐标，利用两点间的距离公式求出弦长．（2）几何法：将两圆作差得到公共弦所在直线方程，利用其中一个圆的圆心和半径，求得该圆心和公共弦所在直线的距离即弦心距，在弦心距、弦的一半和半径构成的直角三角形中，利用勾股定理可以求得弦的一半，进而得到公共弦长．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点4圆系方程及其应用技巧具有某些共同性质的圆的集合称为圆系，它们的方程叫作圆系方程。1、过直线与圆的交点的圆系方程是：（）2、以为圆心的同心圆系方程是：；3、与圆同心的圆系方程是；4、过同一定点的圆系方程是．考点一：圆与圆的位置关系判断例1．（23-24高二上·甘肃庆阳·期末）圆：与圆的位置关系为（）A．相交B．内切C．外切D．相离【答案】A【解析】圆的圆心为，半径为；，则圆的圆心为，半径为.两圆心之间的距离，且满足，可知两圆相交.故选：A.【变式1-1】（22-23高二下·上海·期中）圆与圆的位置关系是（）A．相交B．外切C．外离D．内含【答案】B小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解析】的圆心为，半径为1，的圆心为，半径为1，可知两圆圆心距为2，恰好等于两圆半径之和，所以两圆是外切.故选：B【变式1-2】（23-24高二下·广东惠州·月考）若直线与圆相切，则圆与圆（）A．外切B．相交C．内切D．没有公共点【答案】B【解析】直线与圆相切，则圆心到直线的距离等于圆的半径1，即，得.圆的圆心坐标为，半径为，其圆心在圆上，所以两圆相交.故选：B【变式1-3】（23-24高二上·天津·月考）下列圆中与圆相外切的是（）A．B．C．D．【答案】B【解析】圆方程可化为：，可得：圆心，半径.对A：圆心距，半径之和，故两圆不外切；对B：圆心距，半径之和，故两圆外切；对C：圆心距，半径之和，故两圆不外切；对D：圆心距，半径之和，故两圆不外切.故选：B考点二：由圆与圆位置关系求参小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例2.（23-24高二上·山东日照·期末）若两圆：与：外离，则实数的取值范围为（）A．B．C．D．【答案】D【解析】由题意：即：，它的圆心半径分别为，：即：，它的圆心半径分别为，所以圆心距满足，解得，所以.故选：D.【变式2-1】（23-24高二下·浙江·开学考试）若圆与圆只有一个交点，则实数的值可以是（）A．1B．2C．1D．2【答...