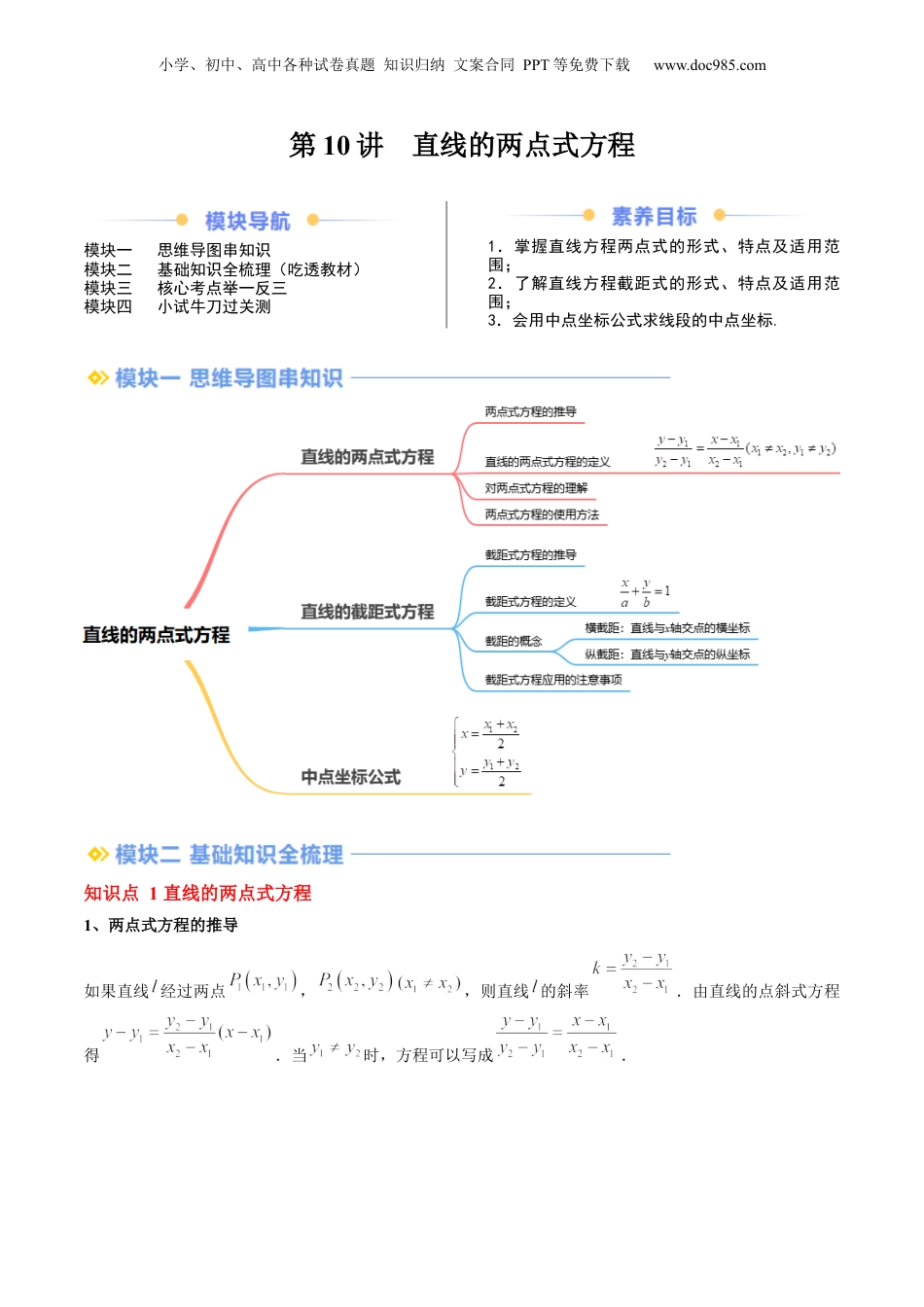
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第10讲直线的两点式方程模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．掌握直线方程两点式的形式、特点及适用范围；2．了解直线方程截距式的形式、特点及适用范围；3．会用中点坐标公式求线段的中点坐标.知识点1直线的两点式方程1、两点式方程的推导如果直线经过两点，，则直线的斜率．由直线的点斜式方程得．当时，方程可以写成．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2、直线的两点式方程定义设直线经过两点，，则方程叫作直线的两点式方程，简称两点式．3、对两点式方程的理解（1）与，显然后者表示直线的范围比前者缩小了，但后者便于记忆和应用，所以采用后者作为公式．（2）对两点式中的两点，只要是直线上的两个不同的点即可，两点式方程与这两个点的顺序无关．（3）把直线的两点式方程化为，则该方程表示过平面内任意不同两点，的直线．4、两点式方程的使用方法（1）已知直线上两点，且，时，可以直接使用该公式求直线方程．（2）当，时，直线方程为或．（3）当，时，直线方程为或．知识点2直线的截距式方程1、截距式方程的推导如图，已知直线经过两点，，其中，有直线的两点式方程得，，即．2、直线的截距式方程的定义小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com设直线在轴的截距为，在轴的截距为，且，则方程叫作直线的截距式方程，简称截距式．3、截距的概念（1）横截距：直线与轴交点的横坐标．在直线方程中，令，解出的值即可．（2）纵截距：直线与轴交点的纵坐标．在直线方程中，令，解出的值即可．4、截距式方程应用的注意事项（1）问题中涉及直线与坐标轴相交，则可考虑截距式方程，用待定系数法确定其系数即可；（2）选用截距式方程时，必须首先考虑直线能否过原点以及能否与两坐标轴垂直；（3）要注意截距式方程的逆向应用．知识点3中点坐标公式若点，的坐标分别为，，且线段的中点M的坐标为，则．考点一：两点式与截距式辨析例1．（23-24高二上·河北邢台·月考）下列直线方程是两点式方程的是（）A．B．C．D．【变式1-1】（2024高二·全国·专题练习）经过两点的直线方程都可以表示为（）A．＝B．＝C．D．＝【变式1-2】（23-24高二上·四川宜宾·月考）（多选）下列说法中错误的是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．直线方程的截距式可表示除过原点外的所有直线B．与是直线的截距式方程C．直线方程的斜截式都可以化为截距式D．在轴、轴上的截距分别是2、的直线方程为【变式1-3】（23-24高二上·江苏宿迁·月考）（多选）下列说法中错误的是（）A．不过原点的直线都可以用方程表示B．若直线，则两直线的斜率相等C．过两点的直线都可用方程表示D．若两条直线中，一条直线的斜率存在，另一条直线的斜率不存在，则两条直线垂直考点二：直线的两点式方程例2.（23-24高二上·宁夏银川·月考）经过点的直线的两点式方程为（）A．B．C．D．【变式2-1】（23-24高二上·内蒙古呼伦贝尔·月考）过点和点的直线的两点式方程是．【变式2-2】（23-24高二上·全国·专题练习）已知三角形的顶点是，求这个三角形三边所在直线的方程.【变式2-3】（23-24高二上·全国·课后作业）已知三个顶点的坐标为，，，求它的对角线AC，BD所在直线的方程.考点三：直线的截距式方程小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例3.（23-24高二上·安徽滁州·期末）在平面直角坐标系中，直线在轴上的截距为（）A．B．8C．D．【变式3-1】（23-24高二上·江苏南京·期末）（多选）过点且在两坐标轴上的截距的绝对值相等的直线方程为（）A．B．C．D．【变式3-2】（23-24高二上·云南昆明·月考）经过点，并且在两坐标轴上的截距相等的直线有（）条.A．0B．1C．2D．3【变式3-3】（23-24高二上·广东东莞·月考）已知直线经过点，斜率为2.(1)求直线的截距式方程.(2)若直线与垂直，且，在y轴上的截距相等，求的截距式...