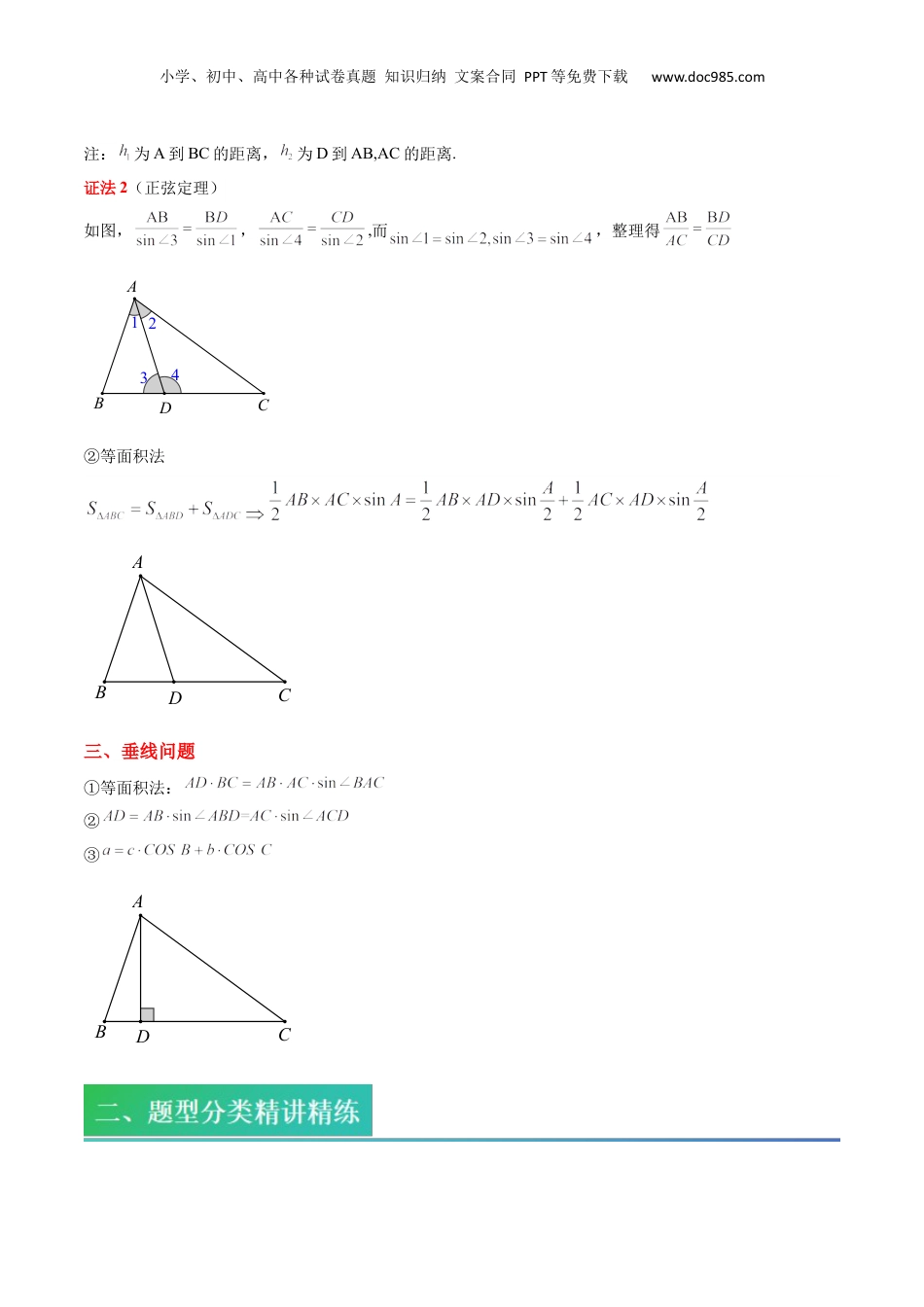
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2024年高二数学暑假自学提升课（人教A版2019选择性必修第一册）复习05讲三角形的中线、垂线、角平分线的应用（精讲+精练）①三角形的中线②三角形的角平分线③三角形的垂线一、中线问题如图，△ABC中，AD为BC的中线，已知AB,AC,及∠A，求中线AD长.DABC②向量法：,平方即可；③余弦定理：邻补角余弦值为相反数，即注：若或将条件“AD为BC的中线”换为“”则可以考虑方法②或方法③.二、角平分线问题ABC△中，AD平分∠BAC.①角平分线定理：证法1（等面积法），得小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com注：为A到BC的距离，为D到AB,AC的距离.证法2（正弦定理）如图，，,而，整理得2143DABC②等面积法DABC三、垂线问题①等面积法：②③DCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com①三角形的中线【题型精练】一、单选题1．（22-23高一下·宁夏银川·阶段练习）如图，已知的内角A，B，C所对的边分别为a，b，c，且，若边上的中线，则的长为（）A．B．C．D．【答案】A【分析】在和中，利用余弦定理建立方程，求解即可.【详解】在中，由余弦定理得，在中，由余弦定理得，相加得，又，解得，故选：A2．（2024·贵州遵义·三模）在中，角的对边分别为，D为的中点，已知，，且，则的面积为（）A．B．C．D．【答案】D小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】先利用正弦定理化边为角求出角，在向量化求出边，再根据三角形的面积公式即可得解.【详解】因为，由正弦定理得，即，又，所以，又，所以，在中，D为的中点，则，则，即，解得（舍去），所以.故选：D.3．（23-24高一下·江苏无锡·阶段练习）在中，，，边上的中线，则的面积S为()A．B．C．D．【答案】C【分析】延长到点使，连接，根据可得面积等于的面积，利用余弦定理求出，再求出sinACE∠，根据三角形面积公式即可求得答案．【详解】如图所示，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com延长到点使，连接，又 ，∴(SAS)，∴的面积等于的面积．在中，由余弦定理得，又，则，∴．故选：C．4．（2023·河南开封·模拟预测）在锐角中，，，则中线的取值范围是（）A．B．C．D．【答案】D【分析】利用正弦定理边化角，结合已知求出边b长的取值范围，再借助平面向量用b表示出中线的长，求出函数值域作答.【详解】令的内角所对边分别为，由正弦定理及得，即，锐角中，，即，同理，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com于是，解得，又线段为边上的中线，则，又，于是，因此，当时，，，所以中线的取值范围是.故选：D二、填空题5．（23-24高一下·重庆·期中）已知的内角的对边分别为，若则边上的中线的长为.【答案】7【分析】利用余弦定理求出，然后由两边平方即可得解.【详解】在中，由余弦定理得，因为为边上的中线，所以，所以，所以，即的长为7.故答案为：7小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com6．（22-23高一下·山东枣庄·期中）中，为边的中线，，，，则中线的长为.【答案】/【分析】先由三角形构建平行四边形，使转化为，然后在根据余弦定理求，即可.【详解】如图，以边,为邻边做平行四边形，因为边的中线，则由平行四边形性质知共线，且，在平行四边形中，，，在中，由余弦定理得：，所以，，故答案为：7．（2023高三·全国·专题练习）在△ABC中，角A，B，C所对的边分别为a，b，c，且，，成等差数列，若，则AC边上中线长的最小值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】【分析】由正弦定理、余弦定理及基本不等式可求解.【详解】 acosC，bcosB，ccosA成等差数列，2bcosB∴＝ccosA+acosC，利用正弦定理得：2sinBcosB=sinCcosA+sinAcosC，整理得：2sinBcosB＝sin（A+C），即2sinBcosB＝sinB， ,sinB≠0∴，∴cosB，则B．如图：设AC边上的中点为E在△BAE中，由余弦定理得：BE2＝c2+（）...