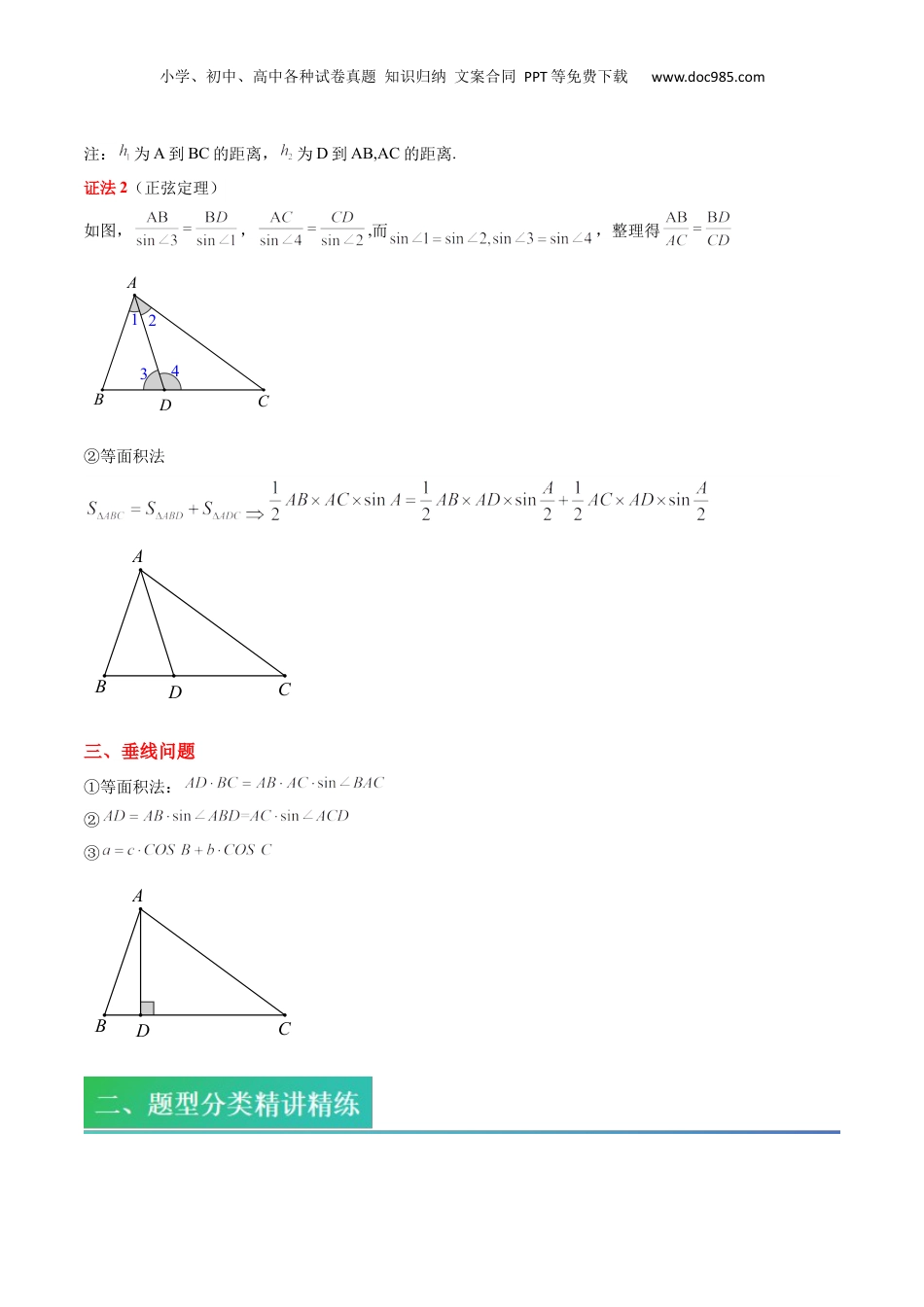
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2024年高二数学暑假自学提升课（人教A版2019选择性必修第一册）复习05讲三角形的中线、垂线、角平分线的应用（精讲+精练）①三角形的中线②三角形的角平分线③三角形的垂线一、中线问题如图，△ABC中，AD为BC的中线，已知AB,AC,及∠A，求中线AD长.DABC②向量法：,平方即可；③余弦定理：邻补角余弦值为相反数，即注：若或将条件“AD为BC的中线”换为“”则可以考虑方法②或方法③.二、角平分线问题ABC△中，AD平分∠BAC.①角平分线定理：证法1（等面积法），得小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com注：为A到BC的距离，为D到AB,AC的距离.证法2（正弦定理）如图，，,而，整理得2143DABC②等面积法DABC三、垂线问题①等面积法：②③DCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com①三角形的中线【题型精练】一、单选题1．（22-23高一下·宁夏银川·阶段练习）如图，已知的内角A，B，C所对的边分别为a，b，c，且，若边上的中线，则的长为（）A．B．C．D．2．（2024·贵州遵义·三模）在中，角的对边分别为，D为的中点，已知，，且，则的面积为（）A．B．C．D．3．（23-24高一下·江苏无锡·阶段练习）在中，，，边上的中线，则的面积S为()A．B．C．D．4．（2023·河南开封·模拟预测）在锐角中，，，则中线的取值范围是（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com二、填空题5．（23-24高一下·重庆·期中）已知的内角的对边分别为，若则边上的中线的长为.6．（22-23高一下·山东枣庄·期中）中，为边的中线，，，，则中线的长为.7．（2023高三·全国·专题练习）在△ABC中，角A，B，C所对的边分别为a，b，c，且，，成等差数列，若，则AC边上中线长的最小值．三、解答题8．（23-24高一下·辽宁·期中）在中，边上的中线．(1)求的长；(2)求的值．9．（2024·山东聊城·三模）在中，内角的对边分别为，且.(1)求；(2)若在边上，且，求的周长.10．（23-24高一下·山东·期中）在中，对应的边分别为，已知向量,且为边上一点，,且.(1)求；(2)求面积的最大值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com②三角形的角平分线【题型精练】一、单选题1．（23-24高一下·重庆·期中）在中，的角平分线交于点，若，，则的面积的最小值为（）A．B．C．D．2．（23-24高三上·福建莆田·期中）在中，B=120°，，A的角平分线，则AC=（）.A．2B．2C．4D．23．（23-24高一下·山东菏泽·期中）在中，为的角平分线，若，，，则（）A．B．C．D．64．（23-24高一下·山东青岛·期中）在中，角A、B、C的对边分别为a，b、c，若，是的角平分线，点在上，，，则（）A．B．C．D．4二、填空题小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．（23-24高一下·江西·期中）在中，点在边上，是的内角的角平分线，，，则的面积是．6．（23-24高一下·江苏无锡·阶段练习）在中，为上一点，①为的中线，则；②为的角平分线，则.7．（22-23高一下·安徽·阶段练习）在中，，是的角平分线，且交于点.若的面积为，则的最大值为.三、解答题8．（23-24高一下·江苏盐城·期中）已知a，b，c分别为三个内角A，B，C的对边，且.(1)求A；(2)已知，的面积为，且AD为角A的角平分线，求线段AD的长.9．（23-24高一下·安徽芜湖·期中）已知的内角的对边为，且.(1)求；(2)若的面积为；（i）已知为的中点，求底边上中线长的最小值；（ii）求内角的角平分线长的最大值.③三角形的垂线小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【题型精练】一、单选题1．（23-24高一下·浙江丽水·期中）已知在中，三个内角的对边分别为，若，，边上的高等于，则的面积为（）A．B．9C．D．2．（2024·安徽·模拟预测）在中，边上的高等于，则（）A．B．C．D．3．（23-24高一下·河南郑州·期中）在中，角所对的边分别是，若，边上的高为，则的最大值为（）A．B．C...