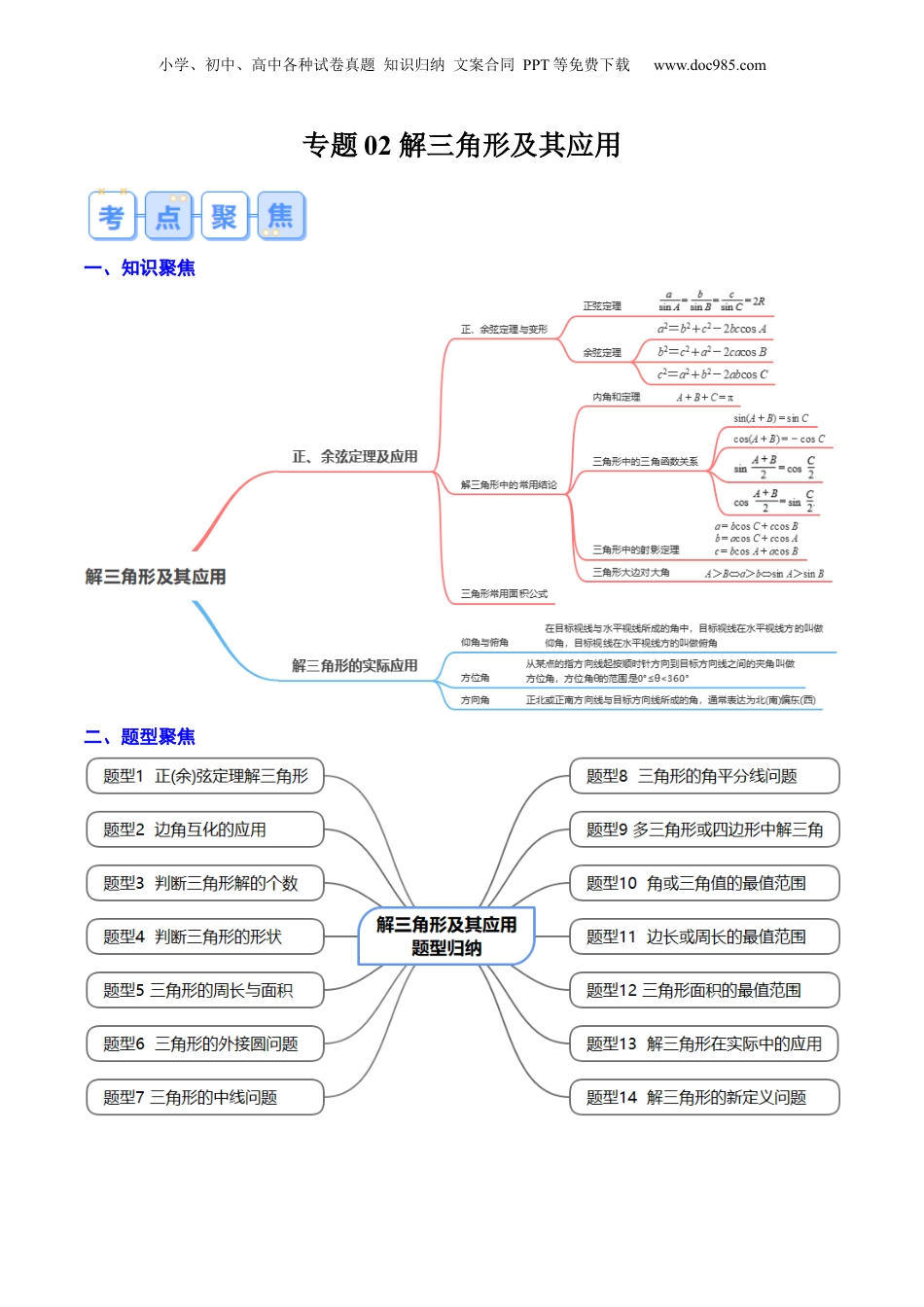
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题02解三角形及其应用一、知识聚焦二、题型聚焦小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点1：正、余弦定理及应用1、正、余弦定理与变形定理正弦定理余弦定理内容＝＝＝2Ra2＝b2＋c2－2bccosA；b2＝c2＋a2－2cacosB；c2＝a2＋b2－2abcosC变形(1)a＝2RsinA，b＝2RsinB，c＝2RsinC；(2)a∶b∶c＝sinA∶sinB∶sinC；(3)＝＝2RcosA＝；cosB＝；cosC＝【注意】若已知两边和其中一边的对角，解三角形时，可用正弦定理．在根据另一边所对角的正弦值确定角的值时，要注意避免增根或漏解，常用的基本方法就是注意结合“大边对大角，大角对大边”及三角形内角和定理去考虑问题．2、解三角形中的常用结论（1）三角形内角和定理：在△ABC中，A＋B＋C＝π；变形：＝－.（2）三角形中的三角函数关系①sin(A＋B)＝sinC；②cos(A＋B)＝－cosC；③sin＝cos；④cos＝sin.（3）三角形中的射影定理：在△ABC中，a＝bcosC＋ccosB；b＝acosC＋ccosA；c＝bcosA＋acosB.（4）三角形中的大角对大边：在△ABC中，A＞B⇔a＞b⇔sinA＞sinB.3、三角形常用面积公式（1）S＝a·ha(ha表示边a上的高)；（2）S＝absinC＝acsinB＝bcsinA；（3）S＝r(a＋b＋c)(r为内切圆半径)．知识点2：解三角形的实际应用名称意义图形表示仰角与俯角在目标视线与水平视线所成的角中，目标视线在水平视线方的叫做仰角，目标视线在水平视线方的叫做俯角方位角从某点的指方向线起按顺时针方向到目标方向线之间的夹角叫做方位角，方位角θ的范围是0°≤θ<360°小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com方向角正北或正南方向线与目标方向线所成的角，通常表达为北(南)偏东(西)例：(1)北偏东α：(2)南偏西α：【注意】（1）方位角和方向角本质上是一样的，方向角是方位角的一种表达形式，是同一问题中对角的不同描述．（2）将三角形的解还原为实际问题时，要注意实际问题中的单位、近似值要求，同时还要注意所求的结果是否符合实际情况．题型归纳【题型1正（余）弦定理解三角形】满分技法解三角时，正余弦定理的选择：（1）已知两角及一边，求其余的边或角，利用正弦定理；（2）已知两边及其一边的对角，求另一边所对的角，利用正弦定理；（3）已知两边及其夹角，求第三边，利用余弦定理；（4）已知三边求角或角的余弦值，利用余弦定理的推论；（5）已知两边及其一边的对角，求另一边，利用余弦定理；1．（23-24高一下·湖南·期中）在中，角所对的边分别为.若，则（）A．2B．4C．16D．2．（23-24高一下·广东广州·期中）在中，，，，则角的值为（）A．B．或C．D．3．（23-24高一下·湖北·月考）中，角A，B，C所对的边分别为已知，则（）A．B．C．D．4．（23-24高一下·重庆·期中）的内角所对边分别为，若，则角的大小（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【题型2边角互化的应用】满分技法边化角是正弦定理齐次比例关系非常重要的应用，其主要特点是将混有边角关系的条件问题转化为三角恒等变换问题,并从角的角度来审视三角形的特征，要熟练掌握边化角的三角形考题的特征,一般来说,当条件中含有特殊数,如(往往和特殊角有关)或者齐次特征明显时，常进行边化角处理对于正弦定理与三角恒等变换的综合问题，大多是基于三角形内角和定理展开的，故一般有两种类型:一是利用相应半角的互余关系、角的互补关系研究三角恒等变换,进而达到减元的目的,也就可以盯着目标进行三角恒等变换:二是利用正弦定理求得相应的角或者寻找相应的边角关系，进而运用三角恒等变换转化为一个角的三角函数问题,5．（23-24高一下·甘肃天水·期中）在△ABC中，角A，B，C所对的边分别为a，b，c，且，，则（）A．B．C．D．6．（23-24高一下·湖北武汉·期中）已知的内角，，的对边分别为，，，且，，则（）A．B．C．D．7．（23-24高一下·四川眉山·月考）在中，角所对的边分别为，已知，且，则（）A．B．C．D．8．（23-24高一下·广西钦州·期中）设的内角的对...