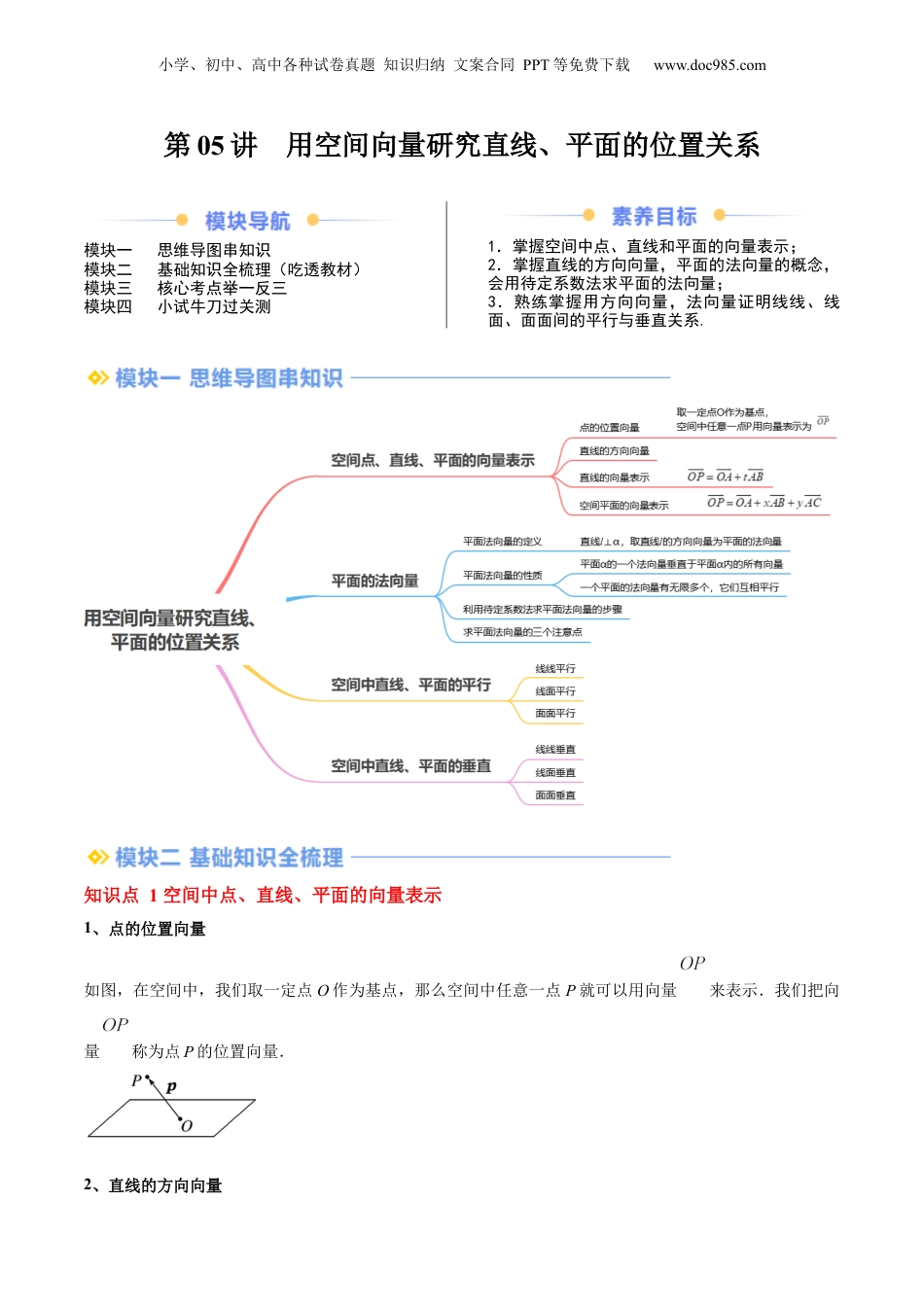
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第05讲用空间向量研究直线、平面的位置关系模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．掌握空间中点、直线和平面的向量表示；2．掌握直线的方向向量，平面的法向量的概念，会用待定系数法求平面的法向量；3．熟练掌握用方向向量，法向量证明线线、线面、面面间的平行与垂直关系.知识点1空间中点、直线、平面的向量表示1、点的位置向量如图，在空间中，我们取一定点O作为基点，那么空间中任意一点P就可以用向量来表示．我们把向量称为点P的位置向量．2、直线的方向向量小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com若A、B是直线上的任意两点，则为直线的一个方向向量；与平行的任意非零向量也是直线的方向向量．【注意】（1）在直线上取有向线段表示的向量，或在与它平行的直线上取有向线段表示的向量，均为直线的方向向量；（2）在解具体立体几何题时，直线的方向向量一般不再叙述而直接应用，可以参与向量运算或向量的坐标运算．3、直线的向量表示直线l的方向向量为，且过点A．如图，取定空间中的任意一点O，可以得到点P在直线l上的充要条件是存在实数t，使①，把代入①式得②，①式和②式都称为空间直线的向量表示式．4、空间平面的向量表示如图（1），设两条直线相交于点，它们的方向向量分别为和，为平面内任意一点，由平面向量基本定理可知，存在唯一的有序实数对，使得．这样，点与向量和不仅可以确定平面，还可以具体表示出内的任意一点．进一步地，如图（2），取定空间任意一点，可以得到，空间一点位于平面内的充要条件是存在实数，使（*）.我们把（*）式称为空间平面的向量表示式．知识点2平面的法向量1、平面法向量的定义如图，若直线，取直线的方向向量，称为平面的法向量；过点A且以为法向量的平面完全确AB�lAB�l小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com定，可以表示为集合．2、平面法向量的性质（1）平面的一个法向量垂直于平面内的所有向量；（2）一个平面的法向量有无限多个，它们互相平行．3、利用待定系数法求平面法向量的步骤（1）设向量：设平面的法向量为n＝(x，y，z)（2）选向量：在平面内选取两个不共线向量AB，AC（3）列方程组：由列出方程组（4）解方程组：（5）赋非零值：取其中一个为非零值(常取±1)（6）得结论：得到平面的一个法向量4、求平面法向量的三个注意点（1）选向量：在选取平面内的向量时，要选取不共线的两个向量（2）取特值：在求n的坐标时，可令x，y，z中一个为一特殊值得另两个值，就是平面的一个法向量（3）注意：提前假定法向量n＝(x，y，z)的某个坐标为某特定值时一定要注意这个坐标不为0．知识点3空间中直线、平面的平行1、线线平行：若分别为直线的方向向量，则使得.2、线面平行：设直线的方向向量，是平面的法向量，，则.法2：在平面内取一个非零向量，若存在实数，使得，且，则.法3：在平面内取两个不共线向量，若存在实数，使得，且，则.3、面面平行：设分别是平面的法向量，则，使得.知识点4空间中直线、平面的垂直1、线线垂直：若分别为直线的方向向量，则.2、线面垂直：设直线的方向向量，是平面的法向量，则，使得.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com法2：在平面内取两个不共线向量，若.则.3、面面垂直：设分别是平面的法向量，则.考点一：直线方向向量的概念与求解例1．（23-24高二上·广东惠州·月考）若，在直线上，则直线的一个方向向量为（）A．B．C．D．【变式1-1】（23-24高二上·青海海东·月考）已知直线l的一个方向向量，且直线l经过和两点，则（）A．B．C．1D．2【变式1-2】（23-24高二上·河北张家口·月考）已知，在直线上，写出直线的一个方向向量：．（坐标表示）【变式1-3】（23-24高二上·宁夏银川·月考）已知向量，都是直线l的方向向量，则x的值是.考点二：平面法向量的概念与求解例2.（22-23高二下·江苏·月考）已知平面上的两个向量，，则平面的一个法向...