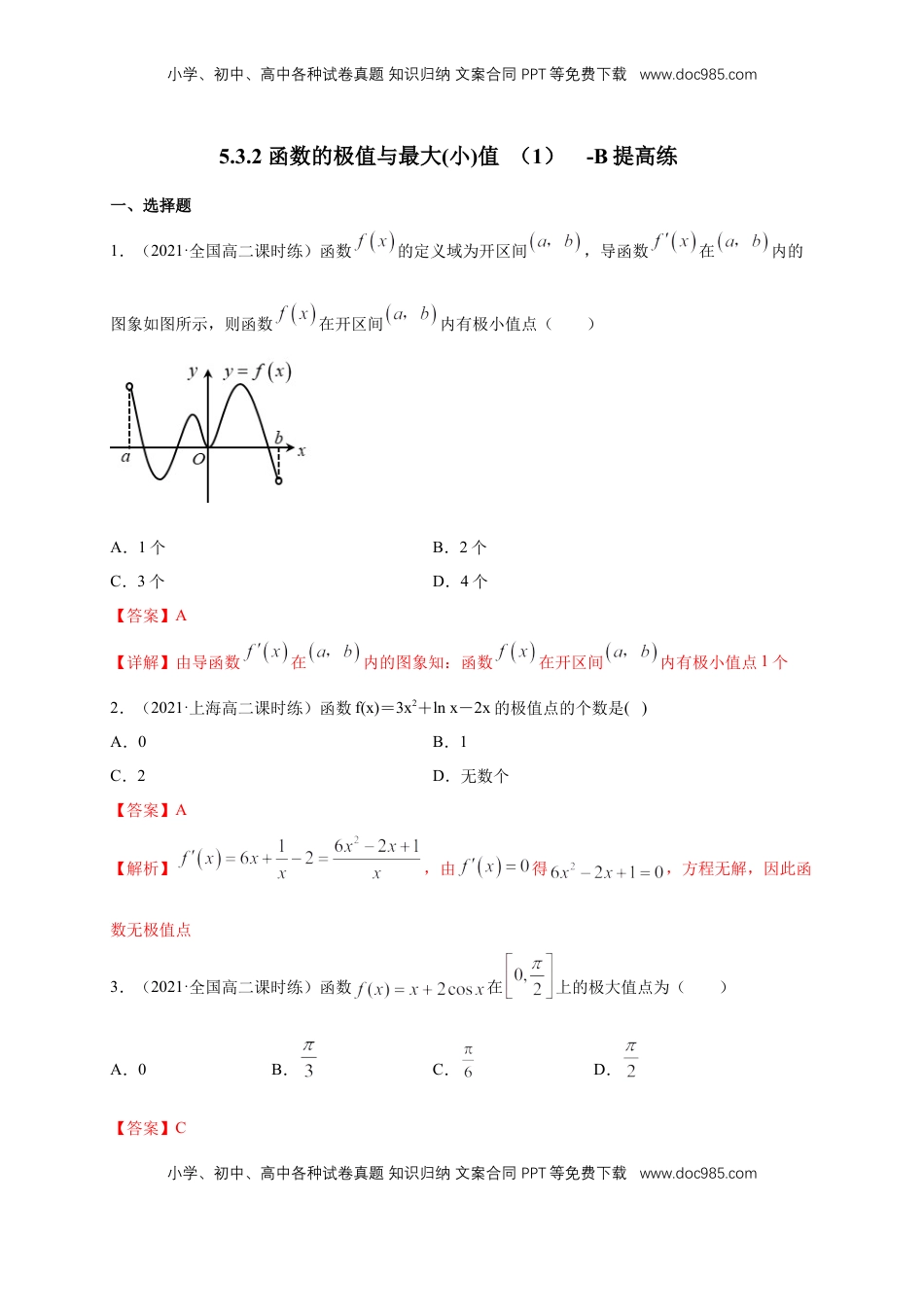
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5.3.2函数的极值与最大(小)值（1）-B提高练一、选择题1．（2021·全国高二课时练）函数的定义域为开区间，导函数在内的图象如图所示，则函数在开区间内有极小值点（）A．1个B．2个C．3个D．4个【答案】A【详解】由导函数在内的图象知：函数在开区间内有极小值点1个2．（2021·上海高二课时练）函数f(x)＝3x2＋lnx－2x的极值点的个数是()A．0B．1C．2D．无数个【答案】A【解析】，由得，方程无解，因此函数无极值点3．（2021·全国高二课时练）函数在上的极大值点为（）A．0B．C．D．【答案】C小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【详解】函数的导数为，令得，又因为，所以，当时，，当时，，所以函数在上单调递增，在上单调递减，所以使得函数取得极大值的的值为，故选：C.4．（2021·全国高二课时练）已知函数的图象与轴相切于点，则的极小值为（）A．B．C．D．【答案】A【详解】由题知，由于函数的图象与轴相切于点，则，解得，，，令，可得或，列表如下：小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com极大值极小值所以，函数的极小值为.故选：A.5．（多选题）（2021·全国高二专题练）已知函数，则下列说法正确的是（）A．有且仅有一个极值点B．有零点C．若的极小值点为，则D．若的极小值点为，则【答案】AC【详解】由题意得，的定义域为，且，设，则，∴在上单调递增，又，，存在唯一零点，设为，当时，单调递减，当时，单调递增，∴有唯一极小值点，故选项A正确．令，得，两边同时取对数可得．∴小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（当且仅当时等号成立），又，∴，即，∴无零点，故选项B错误．由，可设，则．当时，，∴在上单调递减．∴，即，故选项C正确，选项D错误，故选：AC6．（多选题）（2021·湖南省平江一中高二期末）已知，下列说法正确的是（）A．在处的切线方程为B．单调递增区间为C．的极大值为D．方程有两个不同的解【答案】AC【详解】解：因为，所以函数的定义域为，所以，，，∴的图象在点处的切线方程为，即，故A正确；在上，，单调递增，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com在上，，单调递减，故B错误，的极大值也是最大值为，故C正确；方程的解的个数，即为的解的个数，即为函数与图象交点的个数，作出函数与图象如图所示：由图象可知方程只有一个解，故D错误.故选：AC.二、填空题7．（2021·全国高二课时练）已知函数f(x)=x3＋3mx2＋nx＋m2在x=－1时有极值0，则m＋n=________.【答案】11【详解】依题意可得，联立可得或；当时函数，，所以函数在上单调递增，故函数无极值，所以舍去；所以，所以.8．（2021·江西九江高二期末）已知三次函数的图象如图所示，则小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com________．【答案】【详解】解：由题意得，，且，由题图可知，是函数的极大值点，是极小值点，即，是的两个根，由，解得：， ，，∴．9．（2021·广西钦州市·高二期末）已知函数在上存在极值点，则实数a的取值范围是_____________.【答案】或【详解】由题可知：，因为函数在上存在极值点，所以有解所以，则或当或时，函数与轴只有一个交点，即小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以函数在单调递增，没有极值点，故舍...