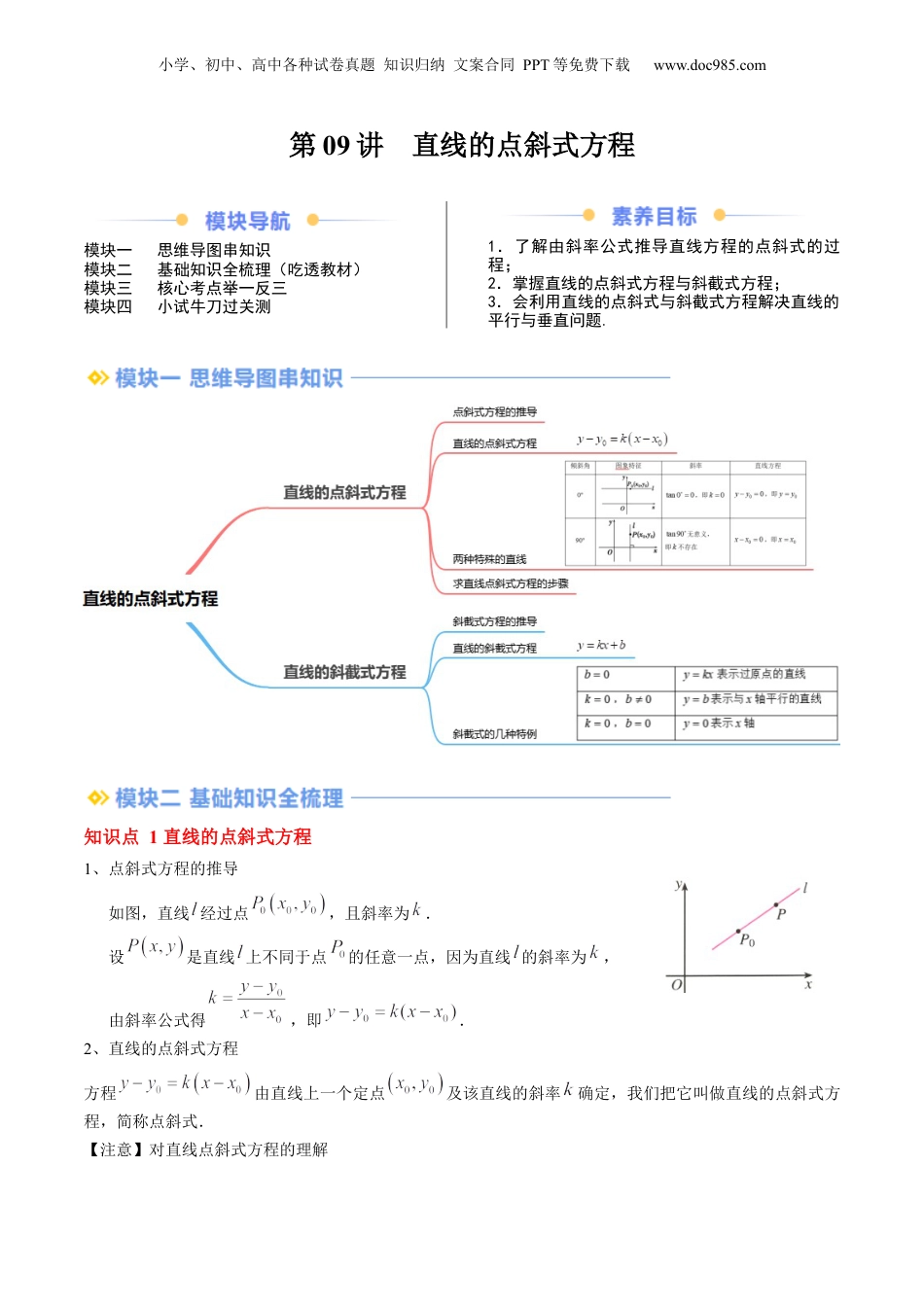
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第09讲直线的点斜式方程模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．了解由斜率公式推导直线方程的点斜式的过程；2．掌握直线的点斜式方程与斜截式方程；3．会利用直线的点斜式与斜截式方程解决直线的平行与垂直问题.知识点1直线的点斜式方程1、点斜式方程的推导如图，直线经过点，且斜率为．设是直线上不同于点的任意一点，因为直线的斜率为，由斜率公式得，即．2、直线的点斜式方程方程由直线上一个定点及该直线的斜率确定，我们把它叫做直线的点斜式方程，简称点斜式．【注意】对直线点斜式方程的理解小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）点斜式的前提条件：①斜率必须存在；②已知直线上一点和直线的斜率．（2）当任意实数时，方程表示恒过定点的无数条直线．3、两种特殊的直线：倾斜角图象特征斜率直线方程0°，即，即90°无意义，即不存在，即4、求直线点斜式方程的一般步骤：（1）求直线点斜式的步骤为：定点定斜率写出方程（2）点斜式方程可表示过点的所有直线，但除外．知识点2直线的斜截式方程1、斜截式方程的推导如图，如果斜率为的直线过点，这时是直线与轴的交点，代入直线的点斜式方程，得，即．2、直线的斜截式方程我们把直线与轴的交点为的纵坐标叫做直线在轴上的截距．这样，方程由直线的斜率与它在轴上的截距确定，我们把方程叫做直线的斜截式方程，简称斜截式．【注意】斜截式方程适用于斜率存在的直线，不能表示斜率不存在的直线，故利用斜截式设直线方程时要讨论斜率是否存在．3、斜截式的几种特例表示过原点的直线，表示与轴平行的直线小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，表示轴考点一：直线的点斜式方程例1．（23-24高二上·江苏苏州·月考）过点且斜率为的直线的点斜式方程为（）A．B．C．D．【答案】B【解析】将，斜率为带入直线方程点斜式，得.故选：B.【变式1-1】（23-24高二下·河南周口·月考）过点且倾斜角为的直线方程为（）A．B．C．D．【答案】B【解析】过点，且倾斜角为的直线斜率为1，则，即．故选：B．【变式1-2】（23-24高二上·全国·课后作业）方程y＝k(x－1)(k∈R)表示()A．过点(－1,0)的一切直线B．过点(1,0)的一切直线C．过点(1,0)且不垂直于x轴的一切直线D．过点(1,0)且除x轴外的一切直线【答案】C【解析】直线的点斜式方程y＝k(x－1)表示经过点(1,0)且斜率为k的直线,显然不垂直于x轴,故选:C.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式1-3】（23-24高二上·云南昭通·期末）已知在平面直角坐标系中，已知的三个顶点为，，，求：(1)所在直线的方程；(2)边上的高所在直线的方程.【答案】(1)；(2).【解析】（1）由，，得直线的斜率为，所以所在直线的方程为，即.（2）由（1）知，直线的斜率为，而，则边上的高所在直线的斜率为，所以直线的方程为，即.考点二：直线的斜截式方程例2.（23-24高二上·江苏宿迁·期中）直线在轴上的截距是（）A．B．C．D．【答案】A【解析】由已知，令，得，所以直线在轴上的截距为，故选：A.【变式2-1】（23-24高二上·全国·课后作业）倾斜角为且在轴上的截距是的直线方程是（）A．B．C．D．【答案】B【解析】倾斜角为，直线的斜率为1，在轴上的截距是，直线方程.故选：B.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式2-2】（23-24高二上·上海奉贤·月考）过点且与直线垂直的直线的斜截式方程是.【答案】【解析】因为直线与直线垂直，所以，解得，所以直线的方程为，化简可得.故答案为：【变式2-3】（23-24高二上·陕西宝鸡·月考）根据条件写出下列直线的斜截式方程.(1)斜率为2，在y轴上的截距是5；(2)倾斜角为，在y轴上的截距是.【答案】(1)；(2).【解析】（1）由直线的斜截式方程知，所求直线方程为.（2）因为直线的倾斜角，则该直线的斜率.所以该直线的斜截式方程为.考点三：直线的图象特征问题例3.（23-...