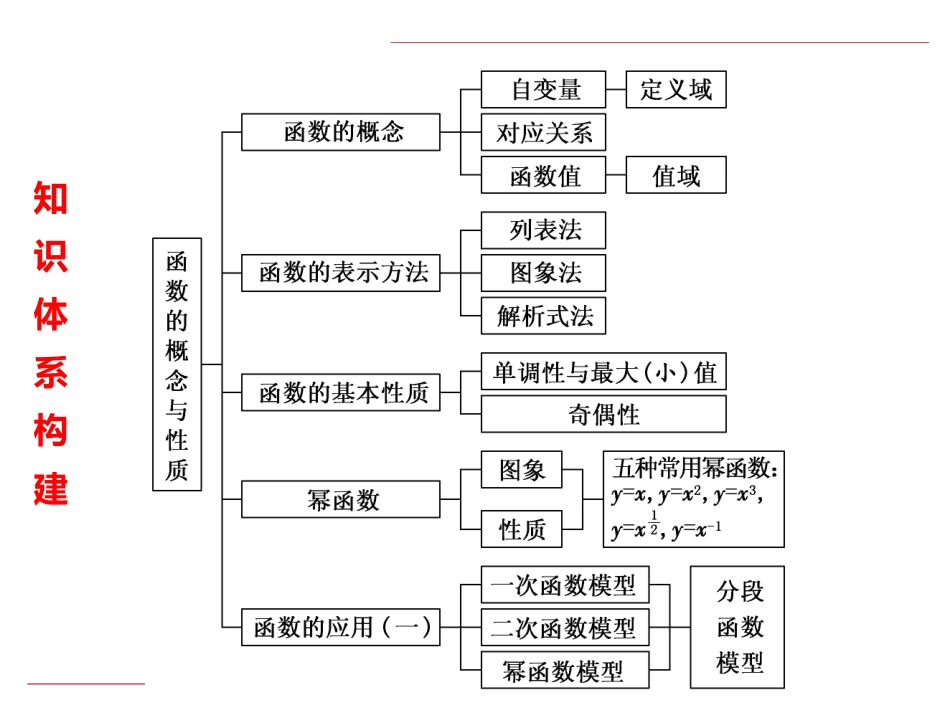
第3章函数的概念与性质学科网知识体系构建[核心素养培优]一、数学运算在本章中数学运算主要体现在函数的定义域和值域求法、函数解析式的求法问题中.函数的定义域[例1](1)函数f(x)＝3x21－x＋(3x－1)0的定义域是()A．－∞，13B．13，1C．－13，13D．－∞，13∪13，1(2)已知函数y＝f(x＋1)的定义域是[－2,3]，则y＝f(2x－1)的定义域是()A．0，52B．[－1,4]C．[－5,5]D．[－3,7][解析](1)由题意得，1－x>0，3x－1≠0，解得x<1且x≠13.(2)设u＝x＋1，由－2≤x≤3，得－1≤x＋1≤4，所以y＝f(u)的定义域为[－1,4]．再由－1≤2x－1≤4，解得0≤x≤52，即函数y＝f(2x－1)的定义域是0，52.[答案](1)D(2)A函数的值域[例2]求下列函数的值域：(1)y＝5x－14x＋2；(2)y＝x2－4x＋32x2－x－1；(3)y＝2x2＋4x－7x2＋2x＋3.[解](1)(借助反比例函数的特征求解)y＝5x－14x＋2＝544x＋2－1－524x＋2＝544x＋2－724x＋2＝54－724x＋2. 724x＋2≠0，∴y≠54.所以函数的值域为y∈Ry≠54.(2) y＝x2－4x＋32x2－x－1＝x－1x－3x－12x＋1＝x－32x＋1(x≠1)，又x－32x＋1＝122x＋1－722x＋1＝12－722x＋1.当x＝1时，原式y＝1－32×1＋1＝－23.∴函数的值域为y∈Ry≠12且y≠－23.(3)(转化为关于x的二次方程，然后利用判别式求值域)已知函数式可变形为：yx2＋2yx＋3y＝2x2＋4x－7.(y－2)x2＋2(y－2)x＋3y＋7＝0，当y≠2时，将上式视为关于x的一元二次方程． x∈R，∴Δ≥0，即[2(y－2)]2－4(y－2)(3y＋7)≥0.解得－92≤y<2.当y＝2时，3×2＋7≠0，∴y≠2.∴函数的值域为－92，2.[例3]已知函数f(x)的值域是14，4，求g(x)＝f(x)－2fx的值域．[解]因为f(x)∈14，4，所以fx∈12，2，设fx＝t∈12，2，所以g(t)＝t2－2t＝(t－1)2－1∈[－1,0]，所以函数g(x)的值域为[－1,0]．函数的解析式[例4](1)已知f(x＋1)＝x2－5x＋4，则f(x)＝________；(2)已知二次函数f(x)满足f(0)＝1，f(1)＝2，f(2)＝5，则该二次函数的解析式为________；(3)若3f(x－1)＋2f(1－x)＝2x，则f(x)的解析式为________．[解析](1)令x＋1＝t，则x＝t－1，因为f(x＋1)＝x2－5x＋4，所以f(t)＝(t－1)2－5(t－1)＋4＝t2－7t＋10，所以f(x)＝x2－7x＋10.(2)设二次函数的解析式为f(x)＝ax2＋bx＋c(a≠0)，由题意得c＝1，a＋b＋c＝2，4a＋2b＋c＝5，解得a＝1，b＝0，c＝1，故f(x)＝x2＋1.(3)令t＝x－1，则x＝t＋1，t∈R，原式变为3f(t)＋2f(－t)＝2(t＋1)，①以－t代替t，①式变为3f(－t)＋2f(t)＝2(1－t)，②由①②消去f(－t)得f(t)＝2t＋25，故f(x)＝2x＋25.[答案](1)x2－7x＋10(2)f(x)＝x2＋1(3)f(x)＝2x＋25二、直观想象直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养，主要表现为：建立形与数的联系，利用几何图形描述问题，借助几何直观理解问题，运用空间想象认识事物．本章主要体现在利用函数的图象研究函数的性质.函数图象的识别及应用[例5](1)已知函数y＝ax2＋bx＋c，如果a>b>c且a＋b＋c＝0，则它的图象可能是()[解析]因为a>b>c且a＋b＋c＝0，所以a>0，c<0，f(1)＝0，则可知开口向上，排除A、C，然后根据f(0)＝c<0，可知函数图象与y轴的交点在x轴下方．[答案]D(2)对于函数f(x)＝x2－2|x|.①判断其奇偶性，并指出图象的对称性；②画此函数的图象，并指出单调区间和最小值．[解]①函数的定义域为R，关于原点对称，f(－x)＝(－x)2－2|－x|＝x2－2|x|.则f(－x)＝f(x)，所以f(x)是偶函数．图象关于y轴对称．②f(x)＝x2－2|x|＝x2－2x＝x－12－1，x≥0，x2＋2x＝x＋12－1，x<0.画出图象如图所示，根据图象知，函数f(x)的最小值是－1.单调递增区间是[－1,0]，[1，＋∞)；单调递减区间是(－∞，－1]，[0,1]．三、逻辑推理在本章中，逻辑推理主要体现在函数单调性、奇偶...