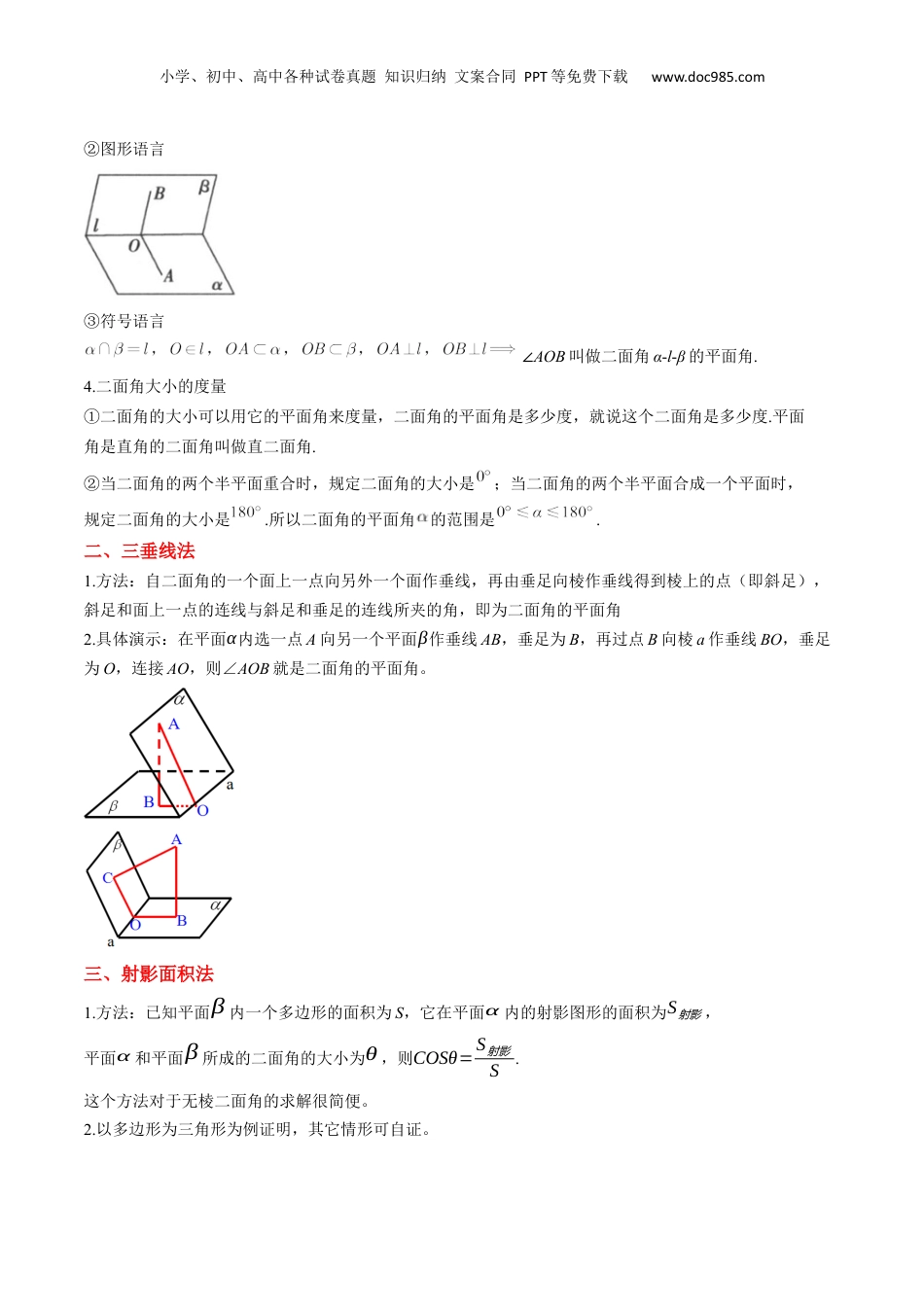
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2024年高二数学暑假自学提升课（人教A版2019选择性必修第一册）复习07讲二面角的常见四大解题方法（精讲+精练）①定义法★②三垂线法③射影面积法④补形法一、二面角定义1.二面角的定义①半平面：平面内的一条直线把平面分成两部分，这两部分通常叫做半平面.②二面角：从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱，这两个半平面叫做二面角的面.2.二面角的表示①棱为AB，面分别为，的二面角记作二面角-AB-，如果棱记作l，那么这个二面角记作二面角-l-，如图(1).②若在，内分别取不在棱上的点P，Q，这个二面角可记作二面角P-AB-Q，如果棱记作l，那么这个二面角记作二面角P-l-Q，如图(2).3.二面角的平面角①自然语言在二面角α-l-β的棱l上任取一点O，以点O为垂足，在半平面α和β内分别作垂直于棱l的射线OA和OB，则射线OA和OB构成的∠AOB叫做二面角的平面角.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com②图形语言③符号语言∠AOB叫做二面角α-l-β的平面角.4.二面角大小的度量①二面角的大小可以用它的平面角来度量，二面角的平面角是多少度，就说这个二面角是多少度.平面角是直角的二面角叫做直二面角.②当二面角的两个半平面重合时，规定二面角的大小是；当二面角的两个半平面合成一个平面时，规定二面角的大小是.所以二面角的平面角的范围是.二、三垂线法1.方法：自二面角的一个面上一点向另外一个面作垂线，再由垂足向棱作垂线得到棱上的点（即斜足），斜足和面上一点的连线与斜足和垂足的连线所夹的角，即为二面角的平面角2.具体演示：在平面α内选一点A向另一个平面β作垂线AB，垂足为B，再过点B向棱a作垂线BO，垂足为O，连接AO，则∠AOB就是二面角的平面角。三、射影面积法1.方法：已知平面β内一个多边形的面积为S，它在平面α内的射影图形的面积为S射影，平面α和平面β所成的二面角的大小为θ，则COSθ=S射影S.这个方法对于无棱二面角的求解很简便。2.以多边形为三角形为例证明，其它情形可自证。小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com证明：如图，平面β内的△ABC在平面α的射影为△A'BC，作AD⊥BC于D，连结AD. AA'⊥α于A'，D∈α，∴AD在α内的射影为A'D.又 AD⊥BC,BC⊂α，∴A'D⊥BC（三垂线定理的逆定理）.∴∠ADA'为二面角α—BC—β的平面角.设△ABC和△A'BC的面积分别为S和S'，∠ADA'=θ，则S=12BC⋅AD,S'=12BC⋅A'D.∴cosθ=A'DAD=12BC⋅A'D12BC⋅AD=S'S.2.点在平面内射影位置的确定立体几何中经常遇到由一个点向一个平面作垂线的问题，垂线的位置由这个点在平面内的射影位置来确定，因此确定这个点的射影位置是解题的关键.一般来说，可以直接过这个点作平面的垂线，然后通过证明或计算说明垂足的位置，也可以借助以下一些常见结论进行确定.(1)如果一个角所在平面外一点到角的两边距离相等，那么这一点在平面内的射影在这个角的平分线上.(2)经过一个角的顶点引这个角所在平面的斜线，如果斜线与这个角的两边的夹角相等，那么该斜线在平面内的射影是这个角的平分线所在直线.四、补形法当构成二面角的两个半平面没有明确交线时，要将两平面的图形补充完整，使之有明确的交线，然后借助前述的定义法与三垂线法解题．①定义法策略方法定义法求二面角的平面角αBDCAA'小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com利用二面角的平面角的定义,在二面角的棱上取一点(特殊点),过该点在两个半平面内作垂直于棱的射线,两射线所成的角就是二面角的平面角,一般地,所涉及的二面角的棱是等腰三角形或正三角形的底边或菱形的对角线以及所求二面角的两个面是全等的三角形等常用此法.【题型精练】一、解答题1．（2024高三·全国·专题练习）如图，在直三棱柱中，，，，点是的中点．(1)求证：平面；(2)求二面角的正切值．2．（23-24高二上·江苏南京·阶段练习）如图，在四棱锥中，平面，四边形为菱形，，，为的中点．(1)求证：平面平面；(2)求二面角的平面角的正弦值．3．...