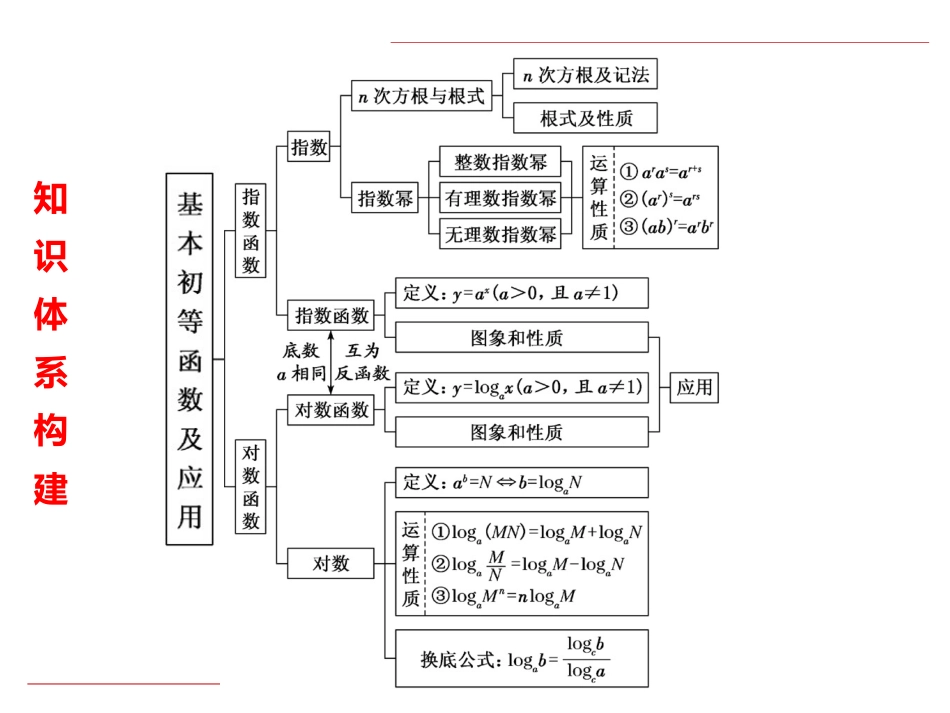
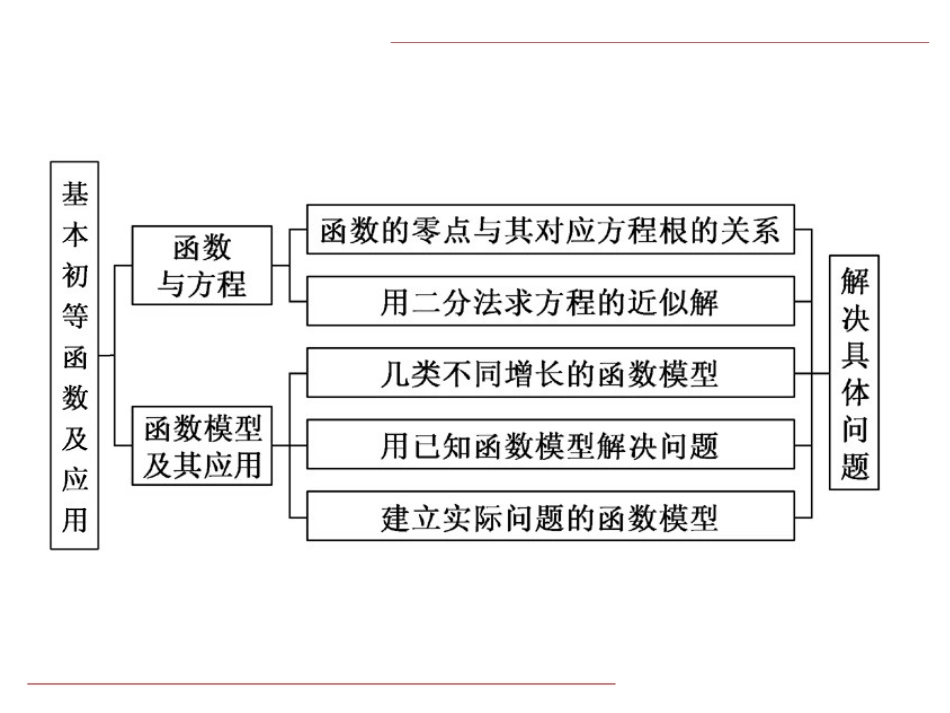
第4章基本初等函数及应用学科网知识体系构建[核心素养培优]一、数学运算数学运算在本章中主要体现在以下三个方面：(1)指数、对数的运算；(2)求函数的零点；(3)函数零点所在区间的判断.指数与对数的运算[例1]求下列各式的值：(1)82723－3e·e23＋2－e2＋10lg2；(2)lg25＋lg2×lg500－12lg125－log29×log32.[解](1)82723－3e·e23＋2－e2＋10lg2＝23323－e13·e23＋(e－2)＋2＝23－2－e＋e－2＋2＝322＝94.(2)lg25＋lg2×lg500－12lg125－log29×log32＝lg25＋lg2×lg5＋2lg2－lg15－log39＝lg5(lg5＋lg2)＋2lg2－lg2＋1－2＝lg5＋lg2－1＝1－1＝0.求函数的零点[例2]已知函数f(x)＝2－|x|，x≤2，x－22，x>2，函数g(x)＝3－f(2－x)，则函数y＝f(x)－g(x)的零点个数为()A．2B．3C．4D．5[解析]函数y＝f(x)－g(x)的零点个数即f(x)，g(x)图象的交点个数．在同一平面直角坐标系中分别画出函数f(x)＝2－|x|，x≤2，x－22，x>2和函数g(x)＝3－f(2－x)的大致图象，如图所示，其中函数g(x)的图象可由f(x)→f(－x)→f(2－x)→－f(2－x)→3－f(2－x)的图象变化得到．由图可知，函数f(x)，g(x)的图象有2个交点，所以函数y＝f(x)－g(x)的零点个数为2.[答案]A函数零点、方程的根所在区间的判断[例3]已知函数f(x)＝6x－log2x，在下列区间中，包含f(x)零点的区间是()A．(0,1)B．(1,2)C．(2,4)D．(4，＋∞)[解析]因为f(x)在(0，＋∞)上为减函数，又f(1)＝6－log21＝6>0，f(2)＝3－log22＝2>0，f(4)＝32－log24＝－12<0，所以由函数零点存在定理知函数f(x)在区间(2,4)内必存在零点．[答案]C二、直观想象在本章中，基本初等函数图象的识别以及根据函数零点的个数求参数等问题均突出体现了直观想象这一核心素养.基本初等函数图象的识别[例4](1)(2019·浙江高考)在同一直角坐标系中，函数y＝1ax，y＝logax＋12(a>0，且a≠1)的图象可能是()(2)若函数y＝logax(a>0，且a≠1)的图象如图所示，则下列函数图象正确的是()[解析](1)当0<a<1时，函数y＝ax的图象过定点(0,1)，在R上单调递减，于是函数y＝1ax的图象过定点(0,1)，在R上单调递增，函数y＝logax＋12的图象过定点12，0，在－12，＋∞上单调递减．因此，选项D中的两个图象符合．当a>1时，函数y＝ax的图象过定点(0,1)，在R上单调递增，于是函数y＝1ax的图象过定点(0,1)，在R上单调递减，函数y＝logax＋12的图象过定点12，0，在－12，＋∞上单调递增．显然A、B、C、D四个选项都不符合．故选D.(2)由题意y＝logax(a>0，且a≠1)的图象过(3,1)点，可解得a＝3.选项A中，y＝3－x＝13x，显然图象错误；选项B中，y＝x3，由幂函数图象可知正确；选项C中，y＝(－x)3＝－x3，显然与所画图象不符；选项D中，y＝log3(－x)的图象与y＝log3x的图象关于y轴对称，显然不符．故选B.[答案](1)D(2)B根据函数零点求参数[例5]定义在R上的偶函数f(x)满足f(x－2)＝f(x＋2)，且当x∈[－2,0]时，f(x)＝12x－1.若关于x的方程f(x)－loga(x＋2)＝0(a>1)在区间(－2,6]上恰有3个不同的实数根，则实数a的取值范围为()A．(1,2)B．(2，＋∞)C．(1，34)D．(34，2)[解析]因为f(x)满足f(x－2)＝f(x＋2)，所以f(x)＝f(x＋4)，所以f(x)是周期为4的周期函数．又f(x)为偶函数，所以f(x)的图象关于y轴对称，画出f(x)与g(x)＝loga(x＋2)的图象，如图所示．因为方程在区间(－2,6]上恰有3个不同的实数根，所以函数f(x)与g(x)的图象恰有3个交点，由图可得g2＝loga4<3，g6＝loga8>3，a>1，解得34<a<2.[答案]D三、逻辑推理本章中，基本初等函数的性质及应用考查了学生的逻辑推理核心素养.比较大小[例6]设a＝30.3，b＝log3310，c＝13－1.6，则a，b，c的大小关系是()A．a<b<cB．b<c<aC．c<b<aD．b<a<c[解析] c＝31.6>30.3＝a>1，b＝log3310<0，∴c>a>b，故选D.[答案]D指数函数、对数函数的性质[例7]设f(x)＝log121－axx－1为奇函数，a为常...