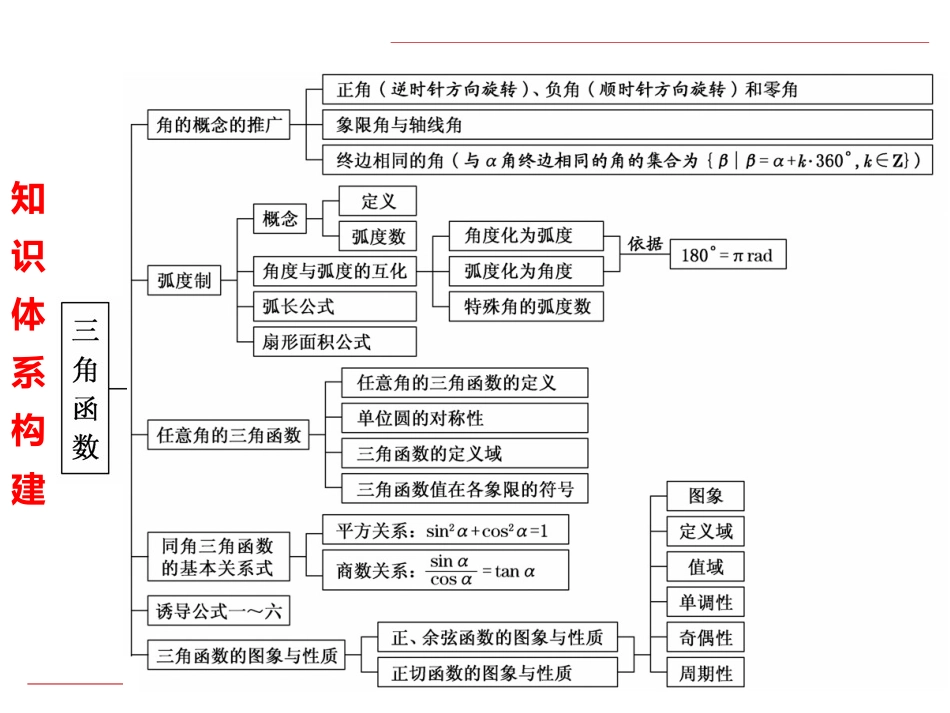
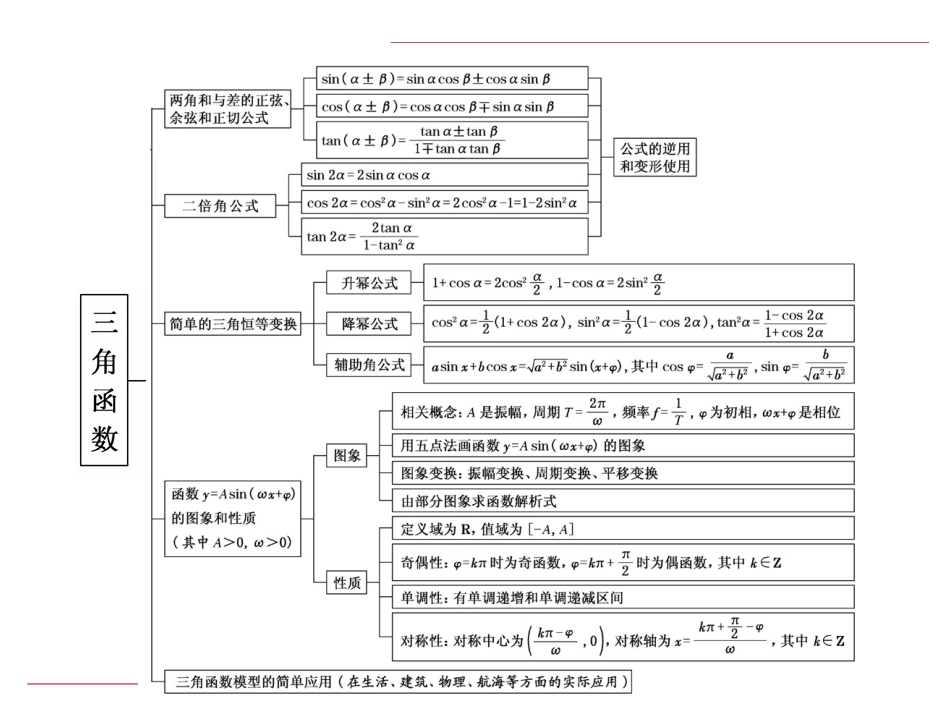
第5章三角函数学科网知识体系构建[核心素养培优]一、数学运算在本章中，通过三角函数的定义域、值域问题以及三角函数求值问题进一步培养提升学生的数学运算核心素养.三角函数的定义域、值域问题[例1](1)函数y＝cosx－12的定义域为______，值域为________．(2)已知f(x)＝2sin2x－π4，x∈R.求函数f(x)在区间π8，3π4上的最小值和最大值．[解析](1)要使函数y＝cosx－12有意义，则cosx－12≥0，即cosx≥12.解得2kπ－π3≤x≤2kπ＋π3，k∈Z.故函数的定义域为2kπ－π3，2kπ＋π3，k∈Z.又－1≤cosx≤1，cosx－12≥0，∴0≤cosx－12≤22，即函数的值域为0，22.[答案]2kπ－π3，2kπ＋π3，k∈Z0，22(2)[解]因为当2kπ－π2≤2x－π4≤2kπ＋π2(k∈Z)，即kπ－π8≤x≤kπ＋3π8(k∈Z)时，函数f(x)＝2sin2x－π4单调递增；当2kπ＋π2≤2x－π4≤2kπ＋3π2(k∈Z)，即kπ＋3π8≤x≤kπ＋7π8(k∈Z)时，函数单调递减，所以f(x)＝2sin2x－π4在区间π8，3π8上为增函数，在区间3π8，3π4上为减函数．又fπ8＝0，f3π8＝2，f3π4＝－1.故函数f(x)在区间π8，3π4上的最大值为2，最小值为－1.利用三角函数的性质求最值[例2](1)函数f(x)＝2cos2x－sin2x＋2的最大值为________．(2)已知函数y＝asin2x＋π6＋b在x∈0，π2上的值域为[－5,1]，求a，b的值．[解析](1) f(x)＝2cos2x－sin2x＋2＝cos2x－sin2x＋122cos2x－1＋52＝cos2x＋12cos2x＋52＝32cos2x＋52∴f(x)的最大值为32＋52＝4.[答案]4(2)[解]因为x∈0，π2，所以2x＋π6∈π6，76π，sin2x＋π6∈－12，1.所以当a＞0时，a＋b＝1，－a2＋b＝－5，解得a＝4，b＝－3，当a＜0时，－a2＋b＝1，a＋b＝－5，解得a＝－4，b＝－1.所以a，b的取值分别是4，－3或－4，－1.给角求值问题[例3]求值：2sin50°＋sin80°1＋3tan10°1＋cos10°.[解]原式＝2sin50°＋2sin80°cos10°12cos10°＋32sin10°2cos5°＝2sin50°＋2sin80°cos10°cos60°－10°2cos5°＝222sin50°＋22cos50°cos5°＝2cos50°－45°cos5°＝2.给值求值问题[例4](1)设α为锐角，若cosα＋π6＝45，求sin2α＋π12的值．(2)已知0＜β＜π2＜α＜π，且cosα－β2＝－19，sinα2－β＝23，求cos(α＋β)的值．[解](1)因为α为锐角且cosα＋π6＝45，所以sinα＋π6＝35.所以sin2α＋π12＝sin2α＋π6－π4＝sin2α＋π6cosπ4－cos2α＋π6sinπ4＝2sinα＋π6cosα＋π6－222cos2α＋π6－1＝2×35×45－22×2×452－1＝12225－7250＝17250.(2)因为0＜β＜π2＜α＜π，所以－π4＜α2－β＜π2，π4＜α－β2＜π，所以cosα2－β＝1－sin2α2－β＝53，sinα－β2＝1－cos2α－β2＝459，所以cosα＋β2＝cosα－β2－α2－β＝cosα－β2cosα2－β＋sinα－β2sinα2－β＝－19×53＋459×23＝7527.所以cos(α＋β)＝2cos2α＋β2－1＝2×49×5729－1＝－239729.给值求角问题[例5]已知0＜α＜π4，0＜β＜π4，且3sinβ＝sin(2α＋β)，4tanα2＝1－tan2α2，求α＋β的值．[解]因为3sinβ＝sin(2α＋β)，即3sin(α＋β－α)＝sin(α＋β＋α)，整理得2sin(α＋β)cosα＝4cos(α＋β)sinα.即tan(α＋β)＝2tanα.又4tanα2＝1－tan2α2，所以tanα＝2tanα21－tan2α2＝12，tan(α＋β)...