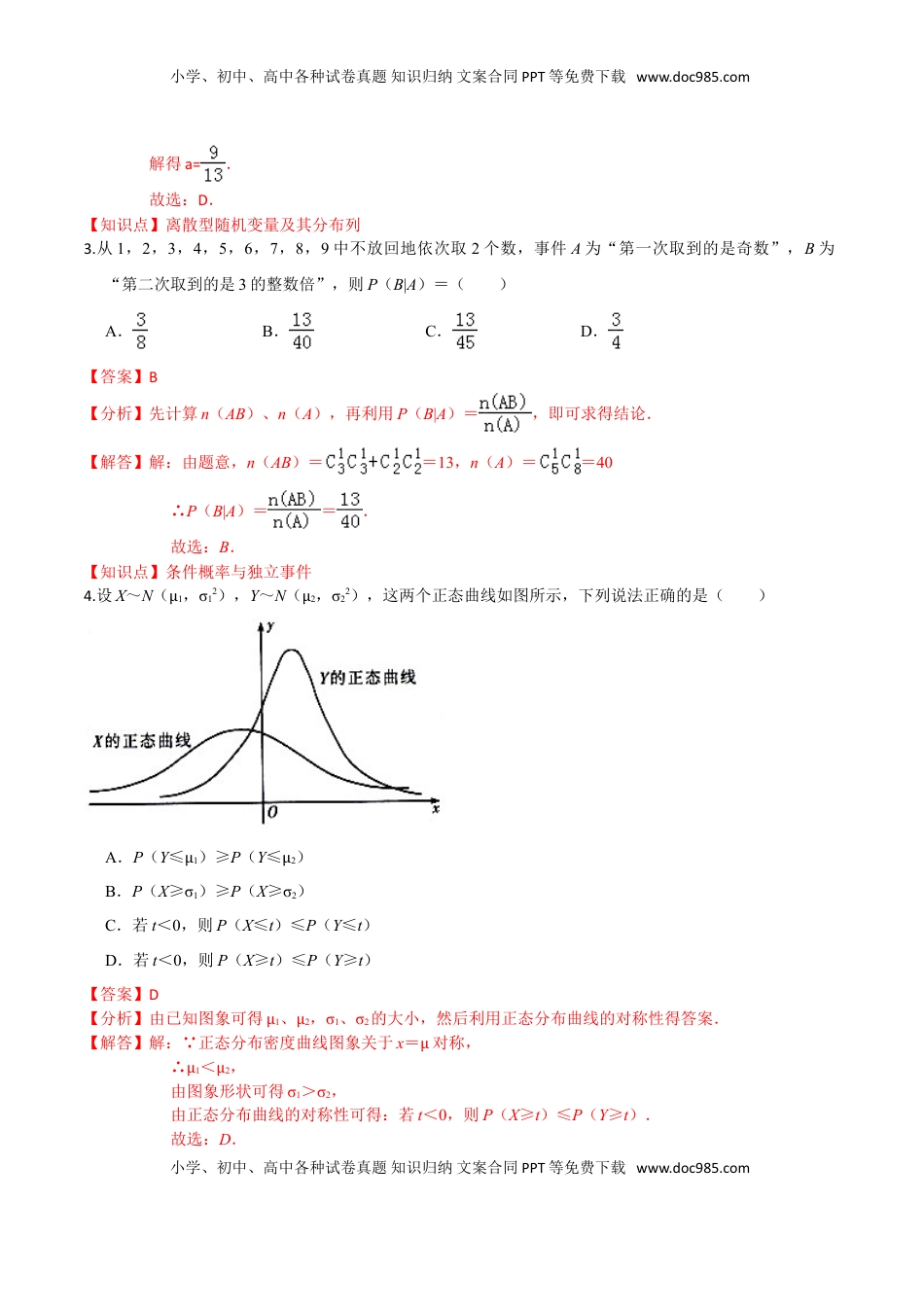
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第七章随机变量及其分布（提高卷）姓名：__________________班级：______________得分：_________________注意事项：本试卷满分150分，考试时间1200分钟，试题共23题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共12小题，每小题5分，共60分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1.随机变量X～B（4，），则D（3X+1）等于（）A．B．C．6D．8【答案】D【分析】判断随机变量X的概率类型，利用二项分布求解方差，然后求解D（3X+1）．【解答】解：由二项分布的概念可知：n＝4，p＝，则：D（X）＝np（1﹣p）＝＝，D（3X+1）＝32D（X）＝9×＝8．故选：D．【知识点】二项分布与n次独立重复试验的模型、离散型随机变量的期望与方差2.设随机变量ξ的概率分布列为P（ξ=k）=a（）k，其中k=0，1，2，那么a的值为（）A．B．C．D．【答案】D【分析】由已知分别求出P（ξ=0），P（ξ=1），P（ξ=2），由此利用离型随机变量的分布列的性质能求出a的值．【解答】解： 随机变量ξ的概率分布列为P（ξ=k）=a（）k，其中k=0，1，2，∴P（ξ=0）==a，P（ξ=1）=a（）=，P（ξ=2）=a（）2=，∴a+=1，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com解得a=．故选：D．【知识点】离散型随机变量及其分布列3.从1，2，3，4，5，6，7，8，9中不放回地依次取2个数，事件A为“第一次取到的是奇数”，B为“第二次取到的是3的整数倍”，则P（B|A）＝（）A．B．C．D．【答案】B【分析】先计算n（AB）、n（A），再利用P（B|A）＝，即可求得结论．【解答】解：由题意，n（AB）＝＝13，n（A）＝＝40∴P（B|A）＝＝．故选：B．【知识点】条件概率与独立事件4.设X～N（μ1，σ12），Y～N（μ2，σ22），这两个正态曲线如图所示，下列说法正确的是（）A．P（Y≤μ1）≥P（Y≤μ2）B．P（X≥σ1）≥P（X≥σ2）C．若t＜0，则P（X≤t）≤P（Y≤t）D．若t＜0，则P（X≥t）≤P（Y≥t）【答案】D【分析】由已知图象可得μ1、μ2，σ1、σ2的大小，然后利用正态分布曲线的对称性得答案．【解答】解： 正态分布密度曲线图象关于x＝μ对称，∴μ1＜μ2，由图象形状可得σ1＞σ2，由正态分布曲线的对称性可得：若t＜0，则P（X≥t）≤P（Y≥t）．故选：D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【知识点】正态分布曲线的特点及曲线所表示的意义5.设10≤x1＜x2＜x3＜x4≤104，x5＝105，随机变量ξ1取值x1、x2、x3、x4、x5的概率均为0.2，随机变量ξ2取值、、、、的概率也均为0.2，若记Dξ1、Dξ2分别为ξ1、ξ2的方差，则（）A．Dξ1＞Dξ2B．Dξ1＝Dξ2C．Dξ1＜Dξ2D．Dξ1与Dξ2的大小关系与x1、x2、x3、x4的取值有关【答案】A【分析】根据随机变量ξ1、ξ2的取值情况，计算它们的平均数，根据随机变量ξ1、ξ2的取值的概率都为0.2，即可求得结论．【解答】解：由随机变量ξ1、ξ2的取值情况，它们的平均数分别为：＝（x1+x2+x3+x4+x5），＝（++++）＝且随机变量ξ1、ξ2的取值的概率都为0.2，所以有Dξ1＞Dξ2，故选：A．【知识点】离散型随机变量及其分布列、离散型随机变量的期望与方差6.设0＜p＜1，随机变量ξ的分布列是ξ012P则当p在（0，1）内增大时，（）A．D（ξ）减小B．D（ξ）增大C．D（ξ）先减小后增大D．D（ξ）先增大后减小【答案】D【分析】求出随机变量ξ的分布列与方差，再讨论D（ξ）的单调情况．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解答】解：设0＜p＜1，随机变量ξ的分布列是E（ξ）＝0×+1×+2×＝p+；方差是D（ξ）＝×+×+×＝﹣p2+p+＝﹣+，∴p∈（0，）时，D（ξ）单调递增；p∈（，1）时，D（ξ）单调...