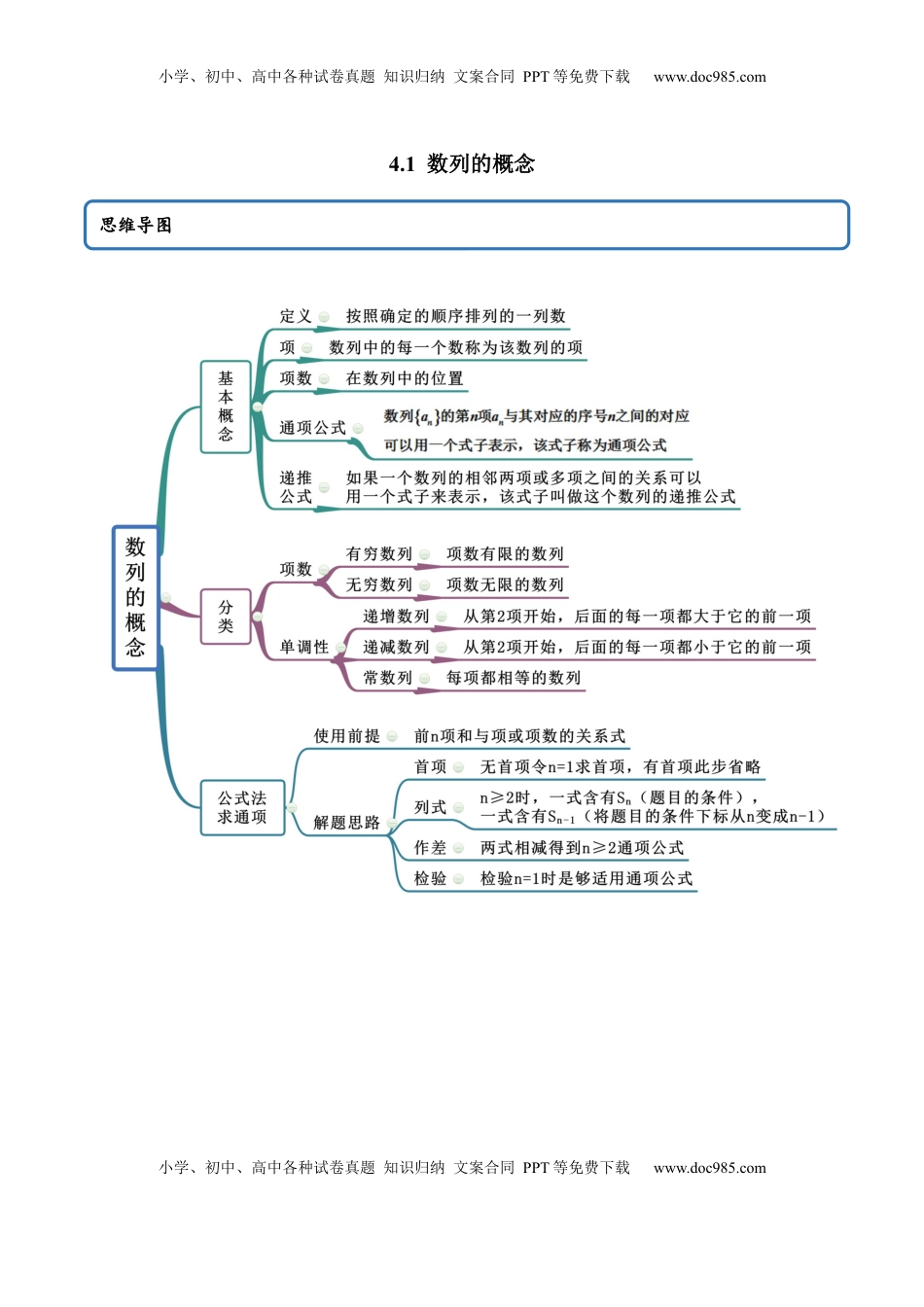
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4.1数列的概念思维导图小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com考法一根据通项求项【例1】（2020·宜宾市南溪区第二中学校）已知数列，则数列的第4项为（）A．B．C．D．【一隅三反】1．（2020·陕西省商丹高新学校期末（文））若数列的通项公式为，则（）A．27B．21C．15D．132．（2020·定远县育才学校月考）已知数列，1，，，，…，，…，则是它的（常见考法小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com）.A．第22项B．第23项C．第24项D．第28项3．（2020·安徽高一期末）已知数列的通项公式为，则的值是（）A．9B．13C．17D．21考法二根据项写通项公式【例2】（2020·邵东县第一中学月考）数列的一个通项公式为（）A．B．C．D．【一隅三反】1．（2020·四川金牛·成都外国语学校高一开学考试（理））数列，3，，，…，则是这个数列的第（）A．8项B．7项C．6项D．5项2（2020·玉龙纳西族自治县田家炳民族中学高一期中）若数列的前项分别是、、、，则此数列一个通项公式为（）A．B．C．D．3．（2020·辽源市第五中学校高一期中（文））数列3，7，13，21，31，…的通项公式是（）A．B．C．D．不存在小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com考法三根据递推公式求项【例3】（2020·湖南省长沙县第九中学期末）数列满足，（为正整数，），则（）A．43B．28C．16D．7【一隅三反】1．（2020·安徽期末）在数列中，，，则（）A．-2B．1C．D．2．（2020·福建厦门·期末）已知数列满足，，则（）A．B．C．D．3．（2020·广西玉林·期末）在数列中，，，则（）A．-2B．2C．1D．-14．（2020·辽源市田家炳高级中学校高一期末（文））数列中，若，，则（）A．29B．2563C．2569D．2557考法四公式法求通项小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例4】（2020·广东广州·期末）已知数列{an}的前项和为，，则数列的通项公式为_____________【一隅三反】1．（2019·陕西省商丹高新学校月考（理））已知数列的前n项和，则______．2．（2020·辽源市田家炳高级中学校高一期末（文））已知数列的前项和为，，且，则数列的通项公式________.3．（2019·内蒙古杭锦后旗奋斗中学高一月考）已知数列的前项和为，则数列的通项公式为_________.考法五斐波那契数列【例5】（2019·浙江）数列：1，1，2，3，5，8，13，21，34，…，称为斐波那契数列，是由十三世纪意大利数学家列昂纳多·斐波那契以兔子繁殖为例子而引入，故又称为“兔子数列”.该数列从第三项开始，每项等于其前相邻两项之和．即：.记该数列的前项和为，则下列结论正确的是（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一隅三反】1.（2020·四川凉山·）一个超级斐波那契数列是一列具有以下性质的正整数:从第三项起，每一项都等于前面所有项之和(例如:1，3，4，8，16…).则首项为2，某一项为2020的超级斐波那契数列的个数为（）A．3B．4C．5D．62．（2020·云南省下关第一中学高二月考（理））“斐波那契数列”由十三世纪意大利数学家列昂纳多·斐波那契发现，因为斐波那契以兔子繁殖为例子而引入，故又称该数列为“兔子数列”.斐波那契数列满足（，），记其前n项和为.设命题，命题，则下列命题为真命题的是（）A．B．C．D．3．（2020·湖北）已知斐波那契数列的前七项为：，大多数植物的花，其花瓣数按层从内向外都恰是斐波那契数．现有层次相同的“雅苏娜”玫瑰花3朵，花瓣总数为99，假设这种“雅苏娜”玫瑰花每层花瓣数由内向外构成斐波那契数列，则一朵该种玫瑰花最可能有（）层．A．5B．6C．7D．8