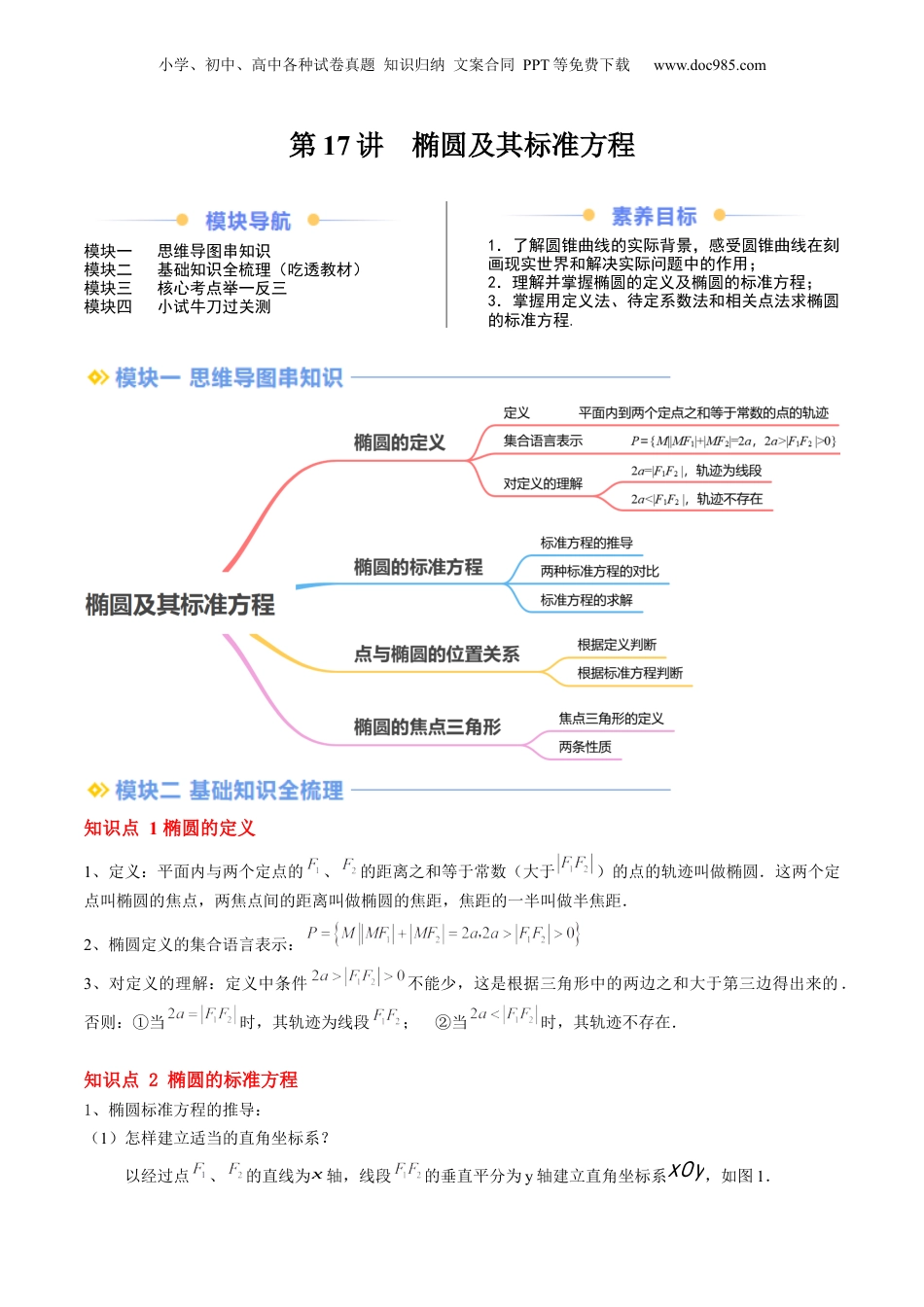
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第17讲椭圆及其标准方程模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．了解圆锥曲线的实际背景，感受圆锥曲线在刻画现实世界和解决实际问题中的作用；2．理解并掌握椭圆的定义及椭圆的标准方程；3．掌握用定义法、待定系数法和相关点法求椭圆的标准方程.知识点1椭圆的定义1、定义：平面内与两个定点的、的距离之和等于常数（大于）的点的轨迹叫做椭圆．这两个定点叫椭圆的焦点，两焦点间的距离叫做椭圆的焦距，焦距的一半叫做半焦距．2、椭圆定义的集合语言表示：3、对定义的理解：定义中条件不能少，这是根据三角形中的两边之和大于第三边得出来的．否则：①当时，其轨迹为线段；②当时，其轨迹不存在．知识点2椭圆的标准方程1、椭圆标准方程的推导：（1）怎样建立适当的直角坐标系？以经过点、的直线为x轴，线段的垂直平分为y轴建立直角坐标系xOy，如图1．yOF1F2xMcc图1小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）椭圆可以看作是哪些点的集合？用坐标如何表示？设点M(x,y)是椭圆上任一点，椭圆的焦距为2c（c＞0）.焦点F1,F2的坐标分别是(−c,0),(c,0)，又设M与F1,F2的距离的和等于常数2a．由椭圆的定义，椭圆就是集合P={M||MF1|+|MF2|=2a}因为，所以（3）遇到根式怎么办？两个根式在同一侧能不能直接平方？即两边平方得整理得再平方并整理得两边同除以得考虑,应有，故设，就有．2、椭圆的标准方程对比3、椭圆标准方程的求解（1）利用待定系数法求椭圆标准方程的步骤①定位：确定焦点在那个坐标轴上；②定量：依据条件及确定的值；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com③写出标准方程．（2）求椭圆方程时，若没有指明焦点位置，一般可设所求方程为；（3）当椭圆过两定点时，常设椭圆方程为，将点的坐标代入，解方程组求得系数．知识点3点与椭圆的位置关系1、根据椭圆的定义判断点与椭圆的位置关系，有如下结论：点P在椭圆内部；点P在椭圆上；点P在椭圆外部．2、对于点与椭圆的位置关系，有如下结论：点在椭圆外；点在椭圆内；点在椭圆上；知识点4椭圆的焦点三角形1、定义：椭圆上一点与椭圆的两个焦点组成的三角形通常称为焦点三角形“”．一般利用椭圆的定义、余弦定理和完全平方公式等知识，建立，，之间的关系，采用整体代入的方法解决焦点三角形的面积、周长及角的有关问题．（设为）2、两条性质性质1：，（两个定义）拓展：的周长为小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com的周长为性质2：（余弦定理）．考点一：椭圆定义及其辨析例1．（23-24高二上·北京延庆·期末）已知是椭圆上的动点，则到椭圆的两个焦点的距离之和为（）A．B．C．D．【变式1-1】（23-24高二下·陕西·开学考试）已知分别是椭圆的左、右焦点，为上的一点，若，则（）A．1B．2C．4D．8【变式1-2】（23-24高二下·安徽·月考）如果动点满足，则点的轨迹是（）A．椭圆B．双曲线C．抛物线D．线段【变式1-3】（23-24高二上·河南焦作·月考）（多选）下列是真命题的是（）A．已知定点，则满足的点的轨迹为椭圆B．已知定点，则满足的点的轨迹为线段C．到定点距离相等的点的轨迹为椭圆D．若点到定点的距离的和等于点到定点的距离的和，则点的轨迹为椭圆小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com考点二：求椭圆的标准方程例2.（23-24高二上·安徽滁州·期末）已知椭圆的一个焦点坐标为，则实数的值为（）A．3B．5C．6D．9【变式2-1】（23-24高二上·吉林·期末）若椭圆焦点在轴上且经过点，焦距为6，则该椭圆的标准方程为（）A．B．C．D．【变式2-2】（23-24高二上·河南南阳·月考）焦点在x轴上，中心为坐标原点，经过点,.则椭圆的标准方程为（）A．B．1C．D．1【变式2-3】（22-23高二上·陕西咸阳·月考）过点且与椭圆有相同焦距的椭圆的标准方程为（）A．B．C．D．或考点三：椭圆方程的参数问题例3.23-24高二下·重庆·月考）已...