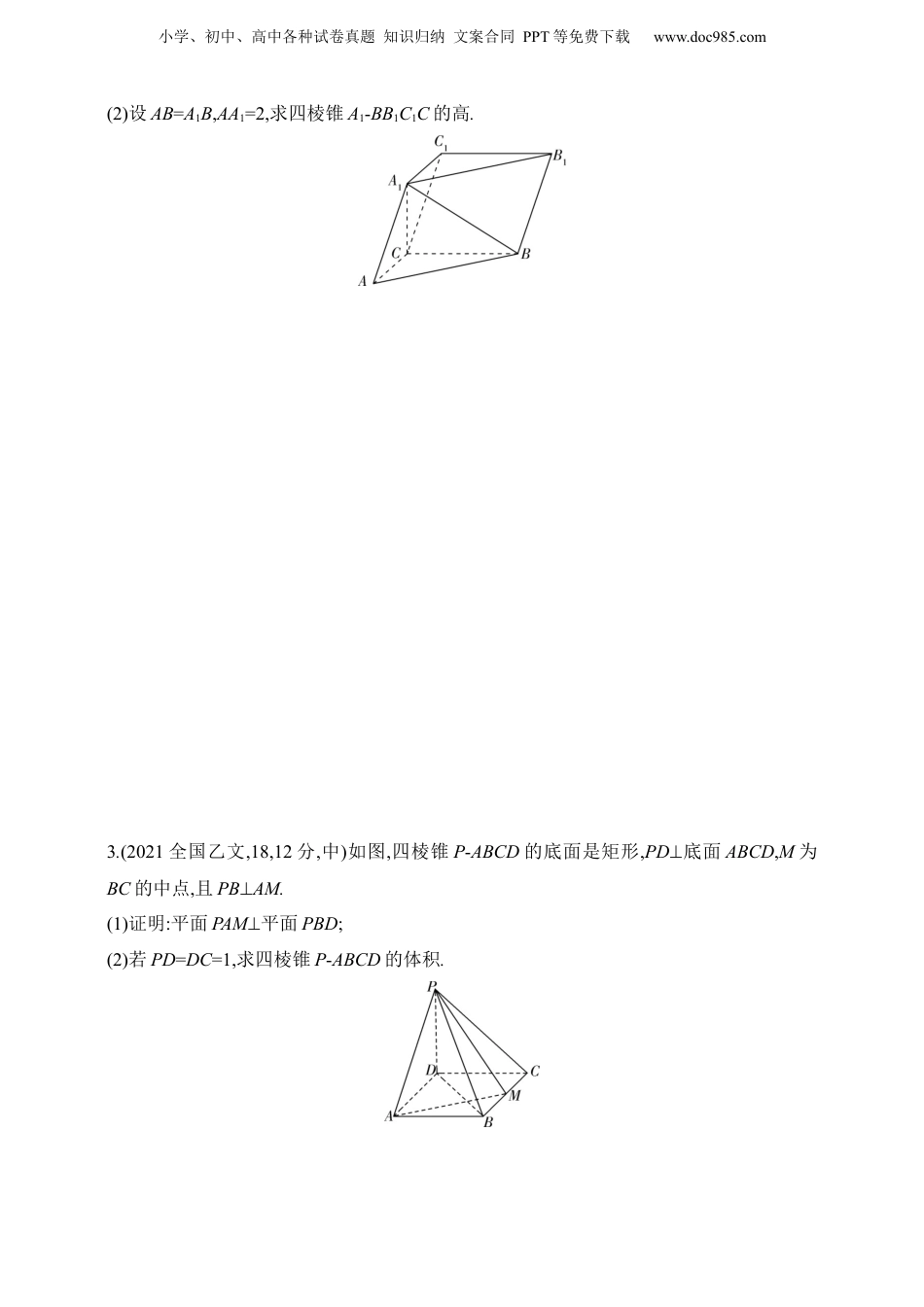
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2025版新教材高考数学第二轮复习7.3直线、平面垂直的判定与性质五年高考高考新风向(2024新课标Ⅱ,17,15分,中)如图,平面四边形ABCD中,AB=8,CD=3,AD=5❑√3,∠ADC=90°,∠BAD=30°,点E,F满足⃗AE=25⃗AD,⃗AF=12⃗AB.将△AEF沿EF翻折至△PEF,使得PC=4❑√3.(1)证明:EF⊥PD;(2)求面PCD与面PBF所成的二面角的正弦值.考点直线、平面垂直的判定与性质1.(2023全国乙文,16,5分,中)已知点S,A,B,C均在半径为2的球面上,△ABC是边长为3的等边三角形,SA⊥平面ABC,则SA=.2.(2023全国甲文,18,12分,中)如图,在三棱柱ABC-A1B1C1中,A1C⊥平面ABC,∠ACB=90°.(1)证明:平面ACC1A1⊥平面BB1C1C;小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(2)设AB=A1B,AA1=2,求四棱锥A1-BB1C1C的高.3.(2021全国乙文,18,12分,中)如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.(1)证明:平面PAM⊥平面PBD;(2)若PD=DC=1,求四棱锥P-ABCD的体积.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4.(2021新高考Ⅰ,20,12分,中)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)证明:OA⊥CD;(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.5.(2020新高考Ⅰ,20,12分,中)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明:l⊥平面PDC;(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com三年模拟练思维1.(2024江苏南通二模,2)在正方体ABCD-A1B1C1D1中,下列关系正确的是()A.AD⊥B1CB.A1D⊥BDC.AC1⊥A1CD.AC1⊥CD12.(2024浙江温州二模,3)在正三棱台ABC-A1B1C1中,下列结论正确的是()A.VABC−A1B1C1=3VA1−BB1C1B.AA1⊥平面AB1C1C.A1B⊥B1CD.AA1⊥BC3.(多选)(2024海南诊断,11)在正方体ABCD-A1B1C1D1中,点P满足λ⃗AP=⃗AB+⃗AD+⃗AA1,其中λ[1,+∞),∈则下列说法正确的是()A.若A,B,D,A1,P在同一球面上,则λ=1B.若AB∥平面A1DP,则λ=2C.若点P到A,B,D,A1四点的距离相等,则λ=3D.若A1P⊥平面PBD,则λ=324.(多选)(2024河北石家庄一模,10)如图,在圆柱O1O中,轴截面ABCD为正方形,点F是´AB上一点,M为BD与轴O1O的交点,E为MB的中点,N为A在DF上的射影,且EF∥平面AMN,则下列选项正确的有()A.CF∥平面AMNB.AN⊥平面DBFC.DB⊥平面AMND.F是´AB的中点5.(2024福建厦门二模,15)如图,三棱柱ABC-A1B1C1中,侧面ABB1A1是边长为2的菱形,∠ABB1=π3,AC=2❑√2,M为A1B1中点,CM=❑√11.(1)证明:平面ABC⊥平面ABB1A1;(2)若BC=2,求平面ABC与平面ABC1夹角的余弦值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com6.(2024湘豫联考第三次模拟,17)如图,在直四棱柱ABCD-A1B1C1D1中,四边形ABCD为菱形,∠ADC=120°,点E,F分别为棱AB,CC1上的点.(1)若⃗AE=λ⃗AB,且平面D1DE⊥平面ABB1A1,求实数λ的值;(2)若F是CC1的中点,平面AB1D1与平面BDF的夹角的余弦值为3❑√1010,求AA1AB的值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com7.(2024浙江杭州二模,17)如图,在多面体ABCDPQ中,底面ABCD是平行四边形,∠DAB=60°,BC=2PQ=4AB=4,M为BC的中点,PQ∥BC,PD⊥DC,QB⊥MD.(1)证明:∠ABQ=90°;(2)若多面体ABCDPQ的体积为152,求平面PCD与平面QAB夹角的余弦值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com8.(2024湖南岳阳二模,15)如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC=2AD=2,E是PC的中点,作EF⊥PB交PB于点F.(1)求证:PB⊥平面DEF;(2)求二面角B-DE-F的正弦值.9.(2024重庆顶级名校3月联考,17)如图,四边形ABCD为矩形,△ACD≌△ACE,且二面角C-AB-E为直二面角.(1)求证:平面ACE⊥平面BCE;(2)设F是BE的中点,AE=1,BE=λ,二面角E-AC-F的平面角的大小为θ,当...