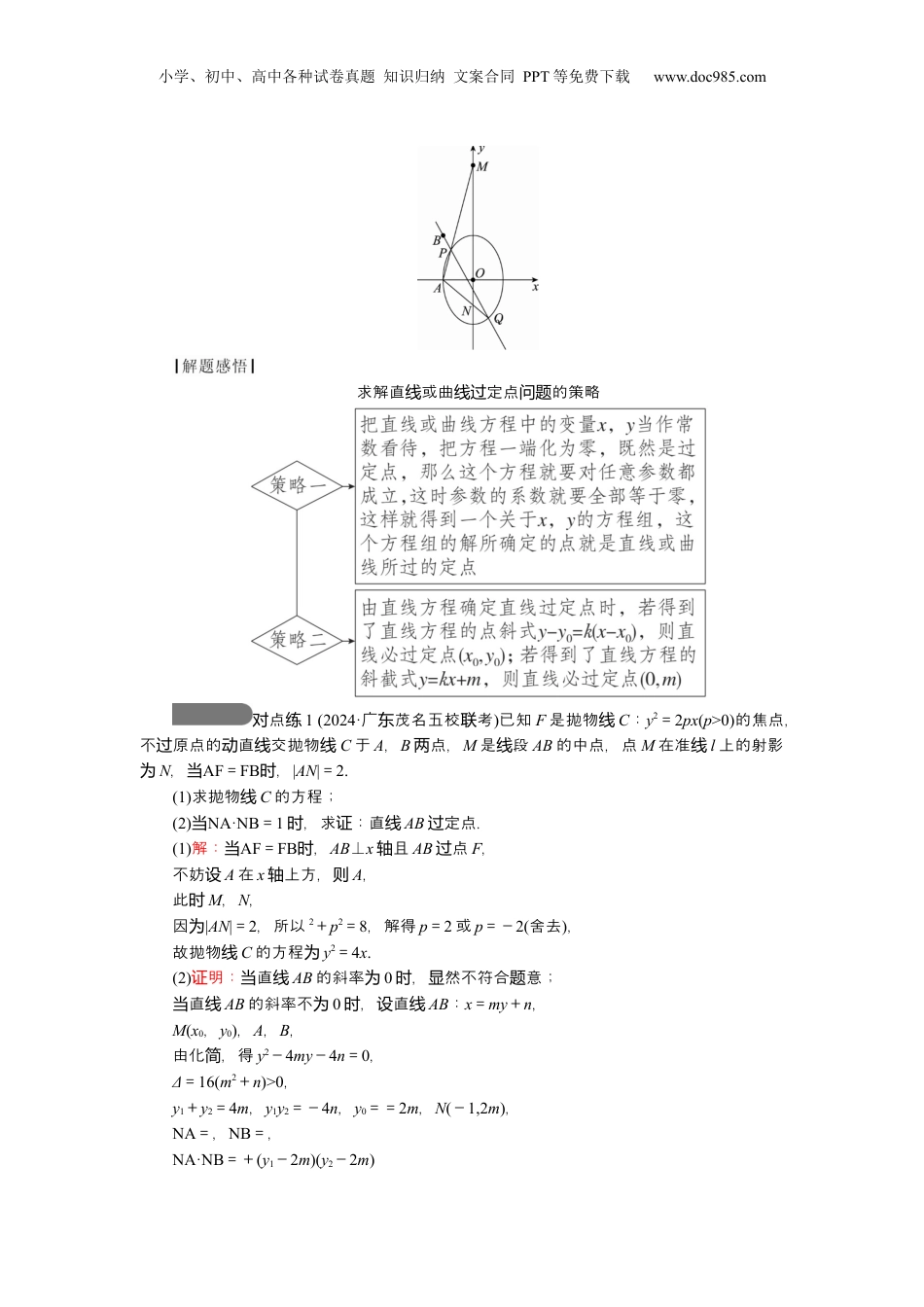
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第11第讲3定点、定课时值问题型题定点问题典例1(2023·全乙卷，理国)已知椭圆C：＋＝1(a>b>0)的离心率，点为A(－2，0)在C上．(1)求C的方程；(2)点过(－2,3)的直交线C于P，Q点，直两线AP，AQ与y的交点分轴别为M，N，证明：段线MN的中点定点．为设P(x1，y1)，Q(x2，y2)，M(0，m)，N(0，n)，＝则kAM＋kAN，又kAM＋kAN＝kAP＋kAQ＝＋，需明：则证kAP＋kAQ＝＋定．为值方法一：次化齐(斜率和问题)．方法二：定比点差法．设PQ＝λBP，即(x2－x1，y2－y1)＝λ(x1＋2，y1－3)，所以x1＝，y1＝，代入4y＋9x＝36得42＋92＝36，①又4y＋9x＝36，②①－②得4(6λy2＋9λ2)＋9(－4λx2＋4λ2)＝36(2λ＋λ2)，即2y2＋3λ－3x2－6＝0，所以＋＝＋＝＝3.(1)解：由意可得解得题所以方程＋＝椭圆为1.(2)明：证由意可知，直题线PQ的斜率存在，直设线PQ为y＝k(x＋2)＋3，P(x1，y1)，Q(x2，y2)，立方程消去联y整理，得并(4k2＋9)x2＋8k(2k＋3)x＋16(k2＋3k)＝0，则Δ＝64k2(2k＋3)2－64(4k2＋9)(k2＋3k)＝－1728k>0，解得k<0，可得x1＋x2＝－，x1x2＝，因为A(－2,0)，直则线AP为y＝(x＋2)，令x＝0，解得y＝，即M，同理可得N，＝＋则＝＝＝＝＝3，所以段线MN的中点是定点(0,3)．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com求解直或曲定点的策略线线过问题点对练1(2024·广茂名五校考东联)已知F是抛物线C：y2＝2px(p>0)的焦点，不原点的直交抛物过动线线C于A，B点，两M是段线AB的中点，点M在准线l上的射影为N，当AF＝FB，时|AN|＝2.(1)求抛物线C的方程；(2)当NA·NB＝1，求：直时证线AB定点．过(1)解：当AF＝FB，时AB⊥x且轴AB点过F，不妨设A在x上方，轴则A，此时M，N，因为|AN|＝2，所以2＋p2＝8，解得p＝2或p＝－2(舍去)，故抛物线C的方程为y2＝4x.(2)明：证直当线AB的斜率为0，然不符合意；时显题直当线AB的斜率不为0，直时设线AB：x＝my＋n，M(x0，y0)，A，B，由化，得简y2－4my－4n＝0，Δ＝16(m2＋n)>0，y1＋y2＝4m，y1y2＝－4n，y0＝＝2m，N(－1,2m)，NA＝，NB＝，NA·NB＝＋(y1－2m)(y2－2m)小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com＝＋＋1＋y1y2－2m(y1＋y2)＋4m2＝n2＋＋1－4n－8m2＋4m2＝n2－2n＋1，若NA·NB＝1，则n2－2n＋1＝1，解得n＝0(舍去)或n＝2，所以直线AB定点过(2,0)．型题定值问题典例2(2024·广佛山考东联)已知P是圆C：(x＋2)2＋y2＝12上一点，定点动M(2,0)，段线PM的垂直平分线n直与线PC交于点T，点记T的迹轨为C′.(1)求C′的方程．(2)若直线l曲与线C′恰有一公共点，且个l直与线l1：y＝x，l2：y＝－x分交于别A，B点，两△OAB的面是不是定积值(O坐原点为标)？若是，求出定；若不是，明理该值请说由．解：(1)由C：(x＋2)2＋y2＝12，可知C(－2,0)，圆C的半径r＝2，接连TM(略图)，因段为线PM的垂直平分线n直与线PC交于点T，所以|TP|＝|TM|，所以|TM|＝|TC|＋2或|TC|＝|TM|＋2，所以||TM|－|TC||＝2<|CM|＝4，所以由曲的定可知，点双线义T的迹是以轨(2,0)，(－2,0)焦点的曲为双线，【方法】合定法和待定系法求解曲的方程，注意定的完性，即总结结义数双线时义备是否完全足曲准方程的件．满双线标条曲方程－＝设双线为1(a>0，b>0)，易知2a＝2，c＝2，所以a＝，c＝2，b＝＝1，所以C′的方程－为y2＝1.(2)直当线l的斜率存在，直时设线l的方程为y＝kx＋m，因直为线l直与线l1：y＝x，l2：y＝－x分交于别A，B点，所以两k≠±.由化整理，简并得(1－3k2)x2－6mkx－3m2－3＝0，因为k≠±，所以1－3k2≠0，因直为线l曲与线C′恰有一公共点，个所以Δ＝36m2k2＋4(1－3k2)(3m2＋3)＝0，即3k2＝m2＋1.由得x＝－，即xA＝－.同理可得xB＝－，则|AB|＝·|xA－xB|＝，又原点O到直线l的距离d＝，所以S△OAB＝|AB|d＝.因为3k2＝m2＋1，所以S△OAB＝.直当线l的斜率不存在时，【方法】本解答先求解直斜率存在的情，再斜率不存在的情充明，总结线况对况补说也可以反，先算斜率不存在的情，容易得到过来计况S△OAB＝，再算斜率存在的情，计况这有一指引的作用．样...