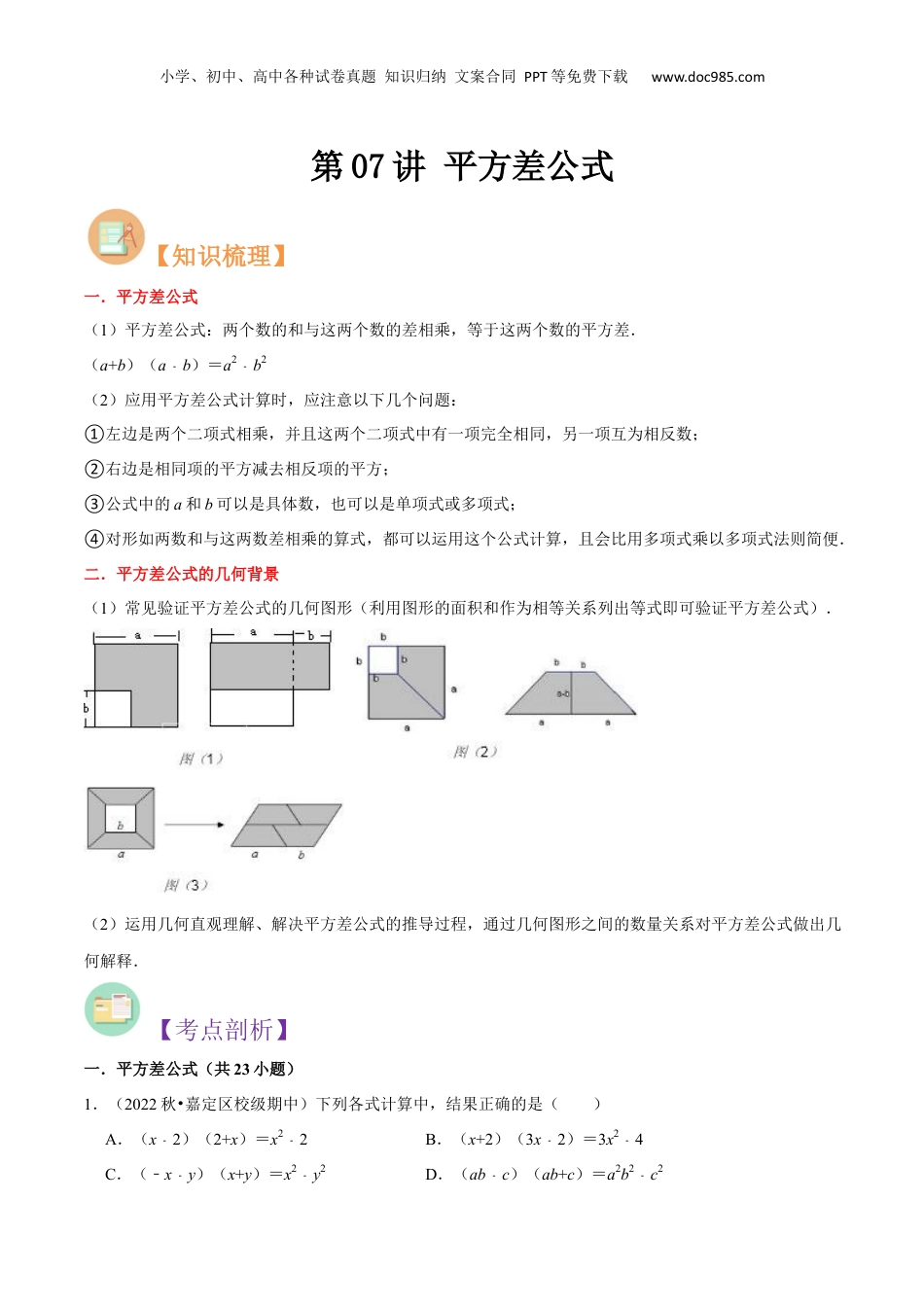
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第07讲平方差公式【知识梳理】一．平方差公式（1）平方差公式：两个数的和与这两个数的差相乘，等于这两个数的平方差．（a+b）（a﹣b）＝a2﹣b2（2）应用平方差公式计算时，应注意以下几个问题：①左边是两个二项式相乘，并且这两个二项式中有一项完全相同，另一项互为相反数；②右边是相同项的平方减去相反项的平方；③公式中的a和b可以是具体数，也可以是单项式或多项式；④对形如两数和与这两数差相乘的算式，都可以运用这个公式计算，且会比用多项式乘以多项式法则简便．二．平方差公式的几何背景（1）常见验证平方差公式的几何图形（利用图形的面积和作为相等关系列出等式即可验证平方差公式）．（2）运用几何直观理解、解决平方差公式的推导过程，通过几何图形之间的数量关系对平方差公式做出几何解释．【考点剖析】一．平方差公式（共23小题）1．（2022秋•嘉定区校级期中）下列各式计算中，结果正确的是（）A．（x2﹣）（2+x）＝x22﹣B．（x+2）（3x2﹣）＝3x24﹣C．（﹣x﹣y）（x+y）＝x2﹣y2D．（ab﹣c）（ab+c）＝a2b2﹣c2小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．（2021秋•徐汇区校级月考）已知（x﹣ay）（x+ay）＝x216﹣y2，那么a＝．3．（2022秋•闵行区期中）计算：（22+1）×（24+1）×（28+1）×（216+1）×（232+1）（结果用幂的形式表示）．4．（2022秋•浦东新区期中）若a＝（﹣1）2022，b＝2021×20232022﹣2，c＝82022×（﹣0.125）2023，则a、b、c的大小关系是（用“＞”连接）．5．（2022秋•宝山区校级期中）计算：＝．6．（2021秋•普陀区校级月考）计算：（2m﹣n）（2m+n）＝．7．（2022秋•上海期末）计算：（x2﹣y）（x+2y）﹣x（x﹣y）．8．（2020秋•普陀区期中）利用公式计算：101×9997﹣29．（2022秋•静安区校级期中）简便运算：198×202．10．（2022秋•闵行区期中）用乘法公式计算：50.2×49.8．11．（2022秋•长宁区校级期中）计算：（1+2a）（12﹣a）（1+4a2）＝．12．（2022秋•黄浦区期中）计算：（2a﹣b）（b+2a）＝．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com13．（2022秋•宝山区校级月考）计算：＝．14．（2022秋•黄浦区期中）计算：（x+1）（x1﹣）（1﹣x2）．15．（2022秋•长宁区校级期中）．16．（2022秋•长宁区校级期中）已知x+y＝7，y＝3，求（x+1）（y+1）（x1﹣）（y1﹣）的值．17．（2022秋•闵行区期中）下列整式乘法能用平方差公式计算的是（）A．（2a+b）（a2﹣b）B．（b2﹣a）（﹣2a﹣b）C．（2a+b）（﹣2a﹣b）D．（a2﹣b）（2b﹣a）18．（2022秋•青浦区校级期中）用乘法公式计算：99×101．19．（2022秋•嘉定区期中）计算：（x2﹣）（x+2）﹣6x（x3﹣）．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com20．（2022秋•浦东新区校级期中）计算：202122020×2022﹣．21．（2022秋•闵行区期中）计算：（3a2﹣b）2（3a+2b）2．22．（2022秋•闵行区期中）利用公式计算：1001×999997﹣2．23．（2022秋•浦东新区期中）计算：＝．二．平方差公式的几何背景（共4小题）24．（2021春•静安区期末）在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证（）A．（a+b）2＝a2+2ab+b2B．（a﹣b）2＝a22﹣ab+b2C．a2﹣b2＝（a+b）（a﹣b）D．（a+2b）（a﹣b）＝a2+ab2﹣b225．（2022秋•黄浦区期中）从边长为a的正方形内去掉一个边长为b的小正方形（如图1），然后将剩余小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com部分剪拼成一个长方形（如图2），上述操作能验证的等式是（）A．（a﹣b）2＝a22﹣ab+b2B．（a+b）2＝a2+2ab+b2C．a2﹣b2＝（a+b）（a﹣b）D．a2+ab＝a（a+b）26．（2020春•庐阳区期末）如图所示，图1是一个边长为a的正方形剪去一个边长为1的小正方形，图2是一个边长为（a1﹣）的正方形，记图1，图2中阴...