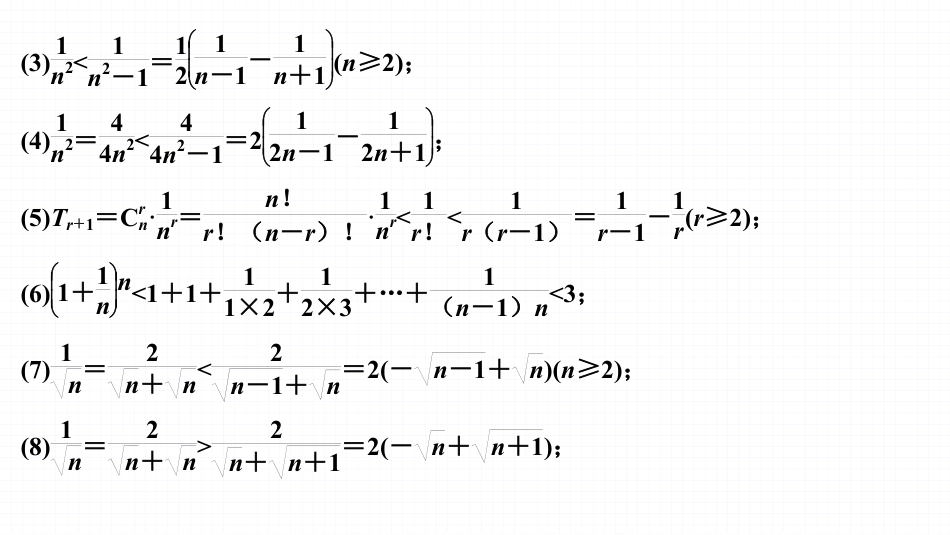板块三数列提优点8数列中的放缩问题知识拓展1.数列放缩是高考重点考查的内容之一，数列与不等式结合试题将稳定在中等偏难的程度，其核心技能是放缩技巧的应用.2.通项放缩常见结论(1)1n2>1n（n＋1）＝1n－1n＋1；(2)1n2<1n2－n＝1n－1－1n(n≥2)；(3)1n2<1n2－1＝121n－1－1n＋1(n≥2)；(4)1n2＝44n2<44n2－1＝212n－1－12n＋1；(5)Tr＋1＝Crn·1nr＝n！r！（n－r）！·1nr<1r！<1r（r－1）＝1r－1－1r(r≥2)；(6)1＋1nn<1＋1＋11×2＋12×3＋…＋1（n－1）n<3；(7)1n＝2n＋n<2n－1＋n＝2(－n－1＋n)(n≥2)；(8)1n＝2n＋n>2n＋n＋1＝2(－n＋n＋1)；(9)1n＝2n＋n<2n－12＋n＋12＝222n－1＋2n＋1＝2(－2n－1＋2n＋1)；(10)2n（2n－1）2＝2n（2n－1）（2n－1）<2n（2n－1）（2n－2）＝2n－1（2n－1）（2n－1－1）＝12n－1－1－12n－1(n≥2)；(11)1n3＝1n·n2<1（n－1）n（n＋1）＝n＋1－n－1（n－1）n（n＋1）·1n＋1－n－1＝1（n－1）n－1n（n＋1）·1n＋1－n－1＝1n－1－1n＋1·n＋1＋n－12n<21n－1－1n＋1(n≥2)；(12)1n3＝2n2·n＋n·n2<2nn－1＋（n－1）n＝2（n－1）n（n＋n－1）＝2（n－n－1）（n－1）n＝2n－1－2n(n≥2)；(13)12n－1＝1（1＋1）n－1<1C0n＋C1n＋C2n－1＝2n（n＋1）＝2n－2n＋1；(14)12n－1<2n－1（2n－1－1）（2n－1）＝12n－1－1－12n－1(n≥2).精准强化练类型一先求和再放缩证明不等式类型二先放缩通项再求和证明不等式类型三通项放缩与求值类型突破类型一先求和再放缩证明不等式对于数列和的不等式，若和易求，一般先求和，再放缩证明.(2024·沈阳模拟)已知数列{an}满足a1＋2a2＋…＋nan＝(n－1)·2n＋1＋2.(1)求{an}的通项公式；由题意可知，当n＝1时，a1＝2；当n≥2时，由a1＋2a2＋…＋nan＝(n－1)·2n＋1＋2得，a1＋2a2＋…＋(n－1)an－1＝(n－2)·2n＋2，两式作差可得，nan＝(n－1)·2n＋1－(n－2)·2n＝n·2n，∴an＝2n，a1＝2也适合该式，故an＝2n.例1(2)设bn＝1an＋1a2n，证明b1＋b2＋…＋bn<43.由题意知bn＝1an＋1a2n＝12n＋14n，故b1＋b2＋…＋bn＝121－12n1－12＋141－14n1－14＝1－12n＋13－13×14n＝43－12n＋13×4n，由于n∈N*，则12n＋13×4n>0，故43－12n＋13×4n<43，即b1＋b2＋…＋bn<43.此类不等式一般另一端为常数，求和以后常利用去项放缩或利用函数的单调性放缩.规律方法训练1(2024·鹰潭模拟)设Sn为数列{an}的前n项和，已知Snn（n＋1）是首项为12、公差为13的等差数列.(1)求{an}的通项公式；因为Snn（n＋1）是首项为12、公差为13的等差数列，故Snn（n＋1）＝12＋13(n－1)＝n3＋16，即Sn＝n3＋16n(n＋1)＝n（2n＋1）（n＋1）6，当n≥2时，Sn－1＝n（2n－1）（n－1）6，故Sn－Sn－1＝an＝n（2n＋1）（n＋1）6－n（2n－1）（n－1）6＝n（2n2＋3n＋1－2n2＋3n－1）6＝n2，当n＝1时，a1＝S1＝3×26＝1，符合上式，故an＝n2.(2)令bn＝（2n－1）anSn，Tn为数列{bn}的前n项积，证明：Tn≤6n－1.由an＝n2，Sn＝n（2n＋1）（n＋1）6，故bn＝（2n－1）anSn＝6（2n－1）n2n（2n＋1）（n＋1）＝6（2n－1）n（2n＋1）（n＋1），则Tn＝b1b2…bn＝6×1×13×2·6×3×25×3·6×5×37×4·…·6（2n－1）n（2n＋1）（n＋1）＝6n（2n＋1）（n＋1），因为(2n＋1)(n＋1)≥3×2＝6，故Tn≤6n6＝6n－1.类型二先放缩通项再求和证明不等式若数列和的不等式不易求和，一般先适当放缩通项，然后累加求和.(2024·丽水调研)设数列{an}的前n项和为Sn，a1＝1，2Sn＝n2＋n(n∈N*).(1)求数列{an}的通项公式；因为2Sn＝n2＋n，①当n≥2时，2Sn－1＝(n－1)2＋n－1，②所以①－②得到2an＝n2＋n－(n－1)2－(n－1)＝2n，即an＝n，又a1＝1，满足an＝n，所以an＝n.例2(2)设数列{bn}的前n项和为Tn，且bn＝1an＋an＋1，求T99；因为bn＝1an＋an＋1＝1n＋n＋1＝n＋1－n，所以T99＝b1＋b2＋…＋b99＝2－1＋3－2＋…＋100－99＝100－1＝9.(3)证明：...