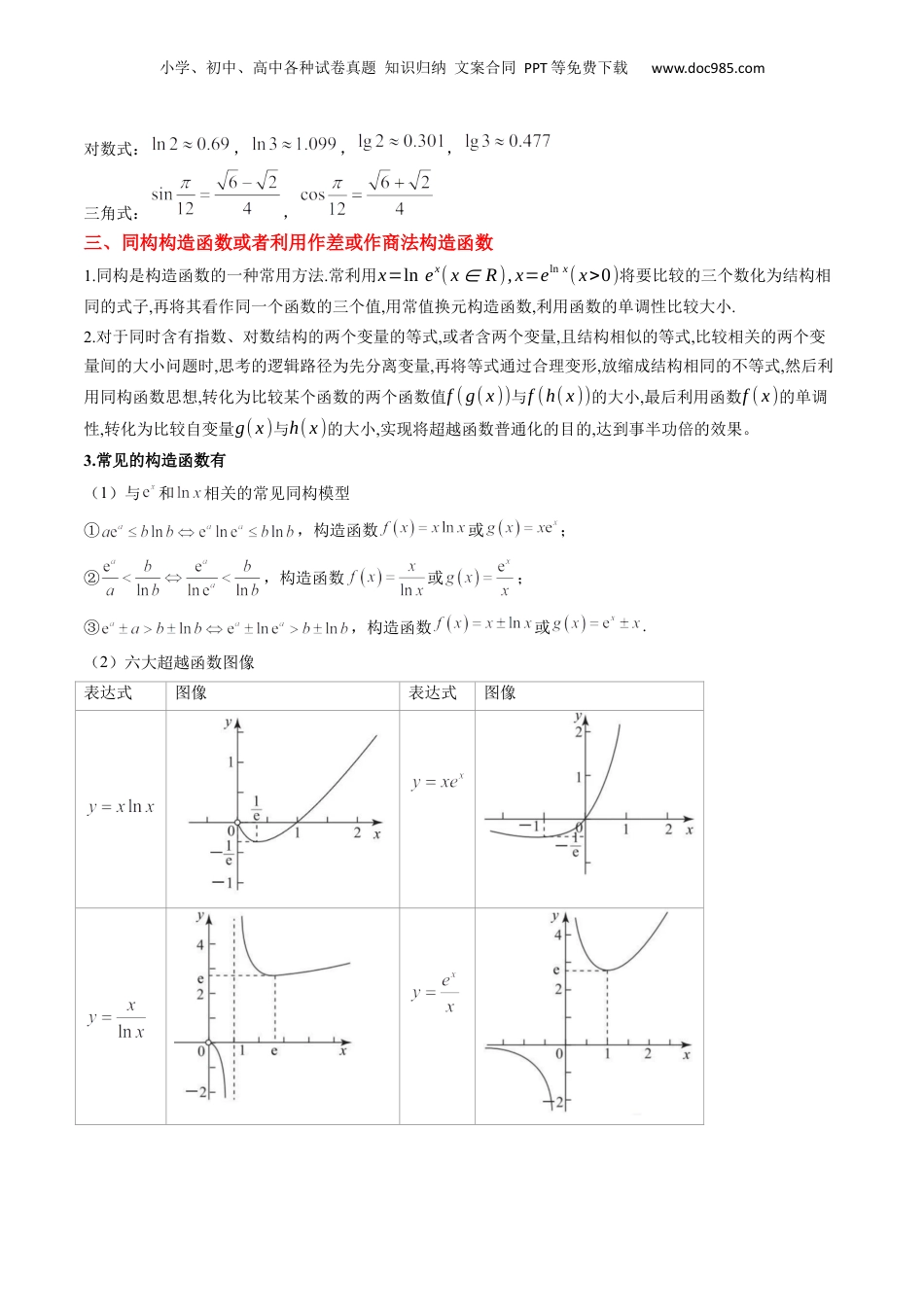
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2025年高考数学一轮复习讲义及高频考点归纳与方法总结（新高考通用）思维拓展04指对幂值的比较大小的常见七大类型（精讲+精练）①利用单调性②作差作商法③利用中间值④利用构造函数⑤数形结合法⑥估算法⑦同构法⑧放缩法一、常规思路1.①底数相同，指数不同时，如和，利用指数函数的单调性；②指数相同，底数不同，如和利用幂函数单调性比较大小；③底数相同，真数不同，如和利用指数函数单调性比较大小；注：除了指对幂函数，其他函数（比如三角函数，对勾函数等）也都可以利用单调性比较大小。2.底数、指数、真数、三角函数名都不同，寻找中间变量0，1或者其它能判断大小关系的中间量，借助“媒介数”进行大小关系的判定.3.通过做差与0的比较来判断两数的大小；通过做商与1的比较来判断两数的大小。二、估值比较大小根式：，，，分式：，指数式：，，一、必备知识整合小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com对数式：，，，三角式：，三、同构构造函数或者利用作差或作商法构造函数1.同构是构造函数的一种常用方法.常利用x=ln⁡ex(x∈R),x=eln⁡x(x>0)将要比较的三个数化为结构相同的式子,再将其看作同一个函数的三个值,用常值换元构造函数,利用函数的单调性比较大小.2.对于同时含有指数、对数结构的两个变量的等式,或者含两个变量,且结构相似的等式,比较相关的两个变量间的大小问题时,思考的逻辑路径为先分离变量,再将等式通过合理变形,放缩成结构相同的不等式,然后利用同构函数思想,转化为比较某个函数的两个函数值f(g(x))与f(h(x))的大小,最后利用函数f(x)的单调性,转化为比较自变量g(x)与h(x)的大小,实现将超越函数普通化的目的,达到事半功倍的效果。3.常见的构造函数有（1）与和相关的常见同构模型①，构造函数或；②，构造函数或；③，构造函数或.（2）六大超越函数图像表达式图像表达式图像小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com三、放缩法常用的放缩不等式（1）；（2）（），当时取等号；变式：,当时取等号；（3）（），当时取等号；变式：；（4）（），当时取等号；（5）（），当时取等号.【典例1】（2024.福建宁德高三统考）设，则的大小关系为（）A．B．C．D．【答案】D【解析】因为以及是上的单调减函数，故可得，，即，；又因为，而是上的单调增函数，则，即.故.故选：D.【典例2】（2023·河南·安阳高中高三模拟）设，，，则a，b、c的大小关系为（）二、考点分类精讲小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】A【分析】利用基本不等式可得，，然后利用换底公式及作差法即得.【详解】 ，，，又，，所以，即，，即，∴.故选：A.【典例3】（2023·天津河东一模）已知，，，则，，的大小顺序为（）A．B．C．D．【答案】C【解析】因为，，，所以.故选：C.【典例4】（2023·江西九江高三专题检测）已知实数a，b，c满足，则a，b，c的大小关系为（）A．B．C．D．【答案】C【解析】由题意知，由，得，设，则，当时，单调递增，因，当且仅当时取等号，故，又，所以，故，∴，则，即有，故.故选:C．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【典例5】（2024·广东广州一模）已知均为大于0的实数，且，则大小关系正确的是（）A．B．C．D．【答案】C【解析】根据题意，将问题转化为函数与直线的交点的横坐标的关系，再作出图像，数形结合求解即可.解：因为均为大于0的实数，所以，进而将问题转化为函数与直线的交点的横坐标的关系，故作出函数图像，如图，由图可知故选：C【典例6】（2023·安徽高三校联考模拟）若，b=1.2，c=ln3.2，则a，b，c的大小关系为（）A．a>b>cB．c>b>aC．a>c>bD．b>a>>c【答案】A【解析】令，则，∴在上单调递增，，即，∴，又，， ，，，故，∴．故选：A．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【典例7】（2023·云南大理高三模拟）若，，，则的大小关系为（）A．B．C．D...