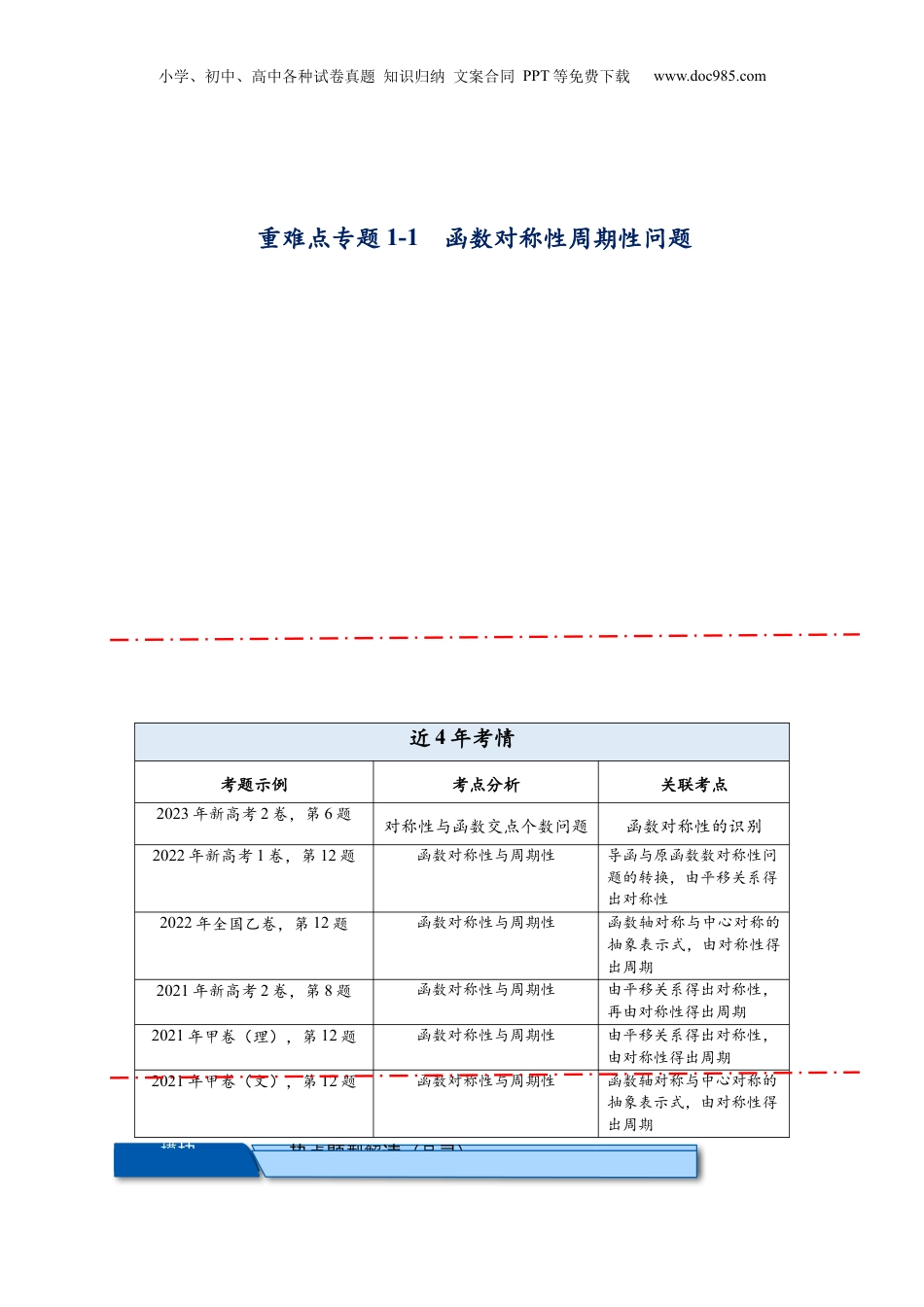
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com重难点专题1-1函数对称性周期性问题近4年考情考题示例考点分析关联考点2023年新高考2卷，第6题对称性与函数交点个数问题函数对称性的识别2022年新高考1卷，第12题函数对称性与周期性导函与原函数数对称性问题的转换，由平移关系得出对称性2022年全国乙卷，第12题函数对称性与周期性函数轴对称与中心对称的抽象表示式，由对称性得出周期2021年新高考2卷，第8题函数对称性与周期性由平移关系得出对称性，再由对称性得出周期2021年甲卷（理），第12题函数对称性与周期性由平移关系得出对称性，由对称性得出周期2021年甲卷（文），第12题函数对称性与周期性函数轴对称与中心对称的抽象表示式，由对称性得出周期点型解（目）热题读录模一块小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com而，故.【巩固练习1】（多选题）已知函数的定义域为，为奇函数，且对于任意，都有，则（）A．B．C．为偶函数D．为奇函数【答案】BCD【解析】由，得．由是奇函数，得，即，所以，即，所以，故选项A错误；由，得，由，得，所以，故选项B正确；由，，得，即为偶函数，故选项C正确；由，，得，则，即为奇函数，故选项D正确．【巩固练习2】已知函数的图象关于点对称，则（）A．1B．2C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【题型2】由对称求解析式一、把的图像关于对称，对称后的函数为，则证明：设对称后的点为，则点在上，故，即二、把的图像关于对称，对称后的函数为，则证明：设对称后的点为，则点在上，代入可得，则有，即2．（2024·四川成都·三模）函数与的图象（）A．关于对称B．关于对称C．关于对称D．关于对称【巩固练习1】若函数y＝g（x）的图象与y＝lnx的图象关于直线x＝2对称，则g（x）＝．【题型3】由平移前后关系得出原函数对称性若已知是奇（偶）函数求对称性是偶函数关于对称，是奇函数关于对称举个例子：若是奇函数证：设关于对称，通过函数图像的平移和伸缩变换求出a，b的值()fmxbc()fx()fmxab()fxxa()fmxab()fx,ab(21)3fx()fxxa()fx(1)fx(21)fx(21)3fx小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com对称中心2024·江苏高邮·统考3．定义在上的函数和的图象关于轴对称，且函数是奇函数，则函数图象的对称中心为（）A．B．C．D．【巩固练习】已知函数的定义域为为偶函数，为奇函数，则（）A．B．C．D．【题型4】与对称性有关的材料题结合材料得出结论，再解决问题4．（多选）在学习了函数的奇偶性后，小明同学发现：函数为奇函数的充要条件是的图象关于坐标原点成中心对称，可以引申为：函数为奇函数的充要条件是的图象关于点成中心对称.已知函数的图象关于成中心对称，则下列结论正确的是（）,ab1,ab1,2ab11,332aabbR()yfx()ygxy(2)1yfx()ygx(2,1)(2,1)(2,1)(2,1)小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【巩固练习1】（多选）已知函数的图象关于成中心对称图形的充要条件是是奇函数，函数的图象关于成轴对称图形的充要条件是是偶函数.则下列说法正确的是（）A．的对称中心为B．关于对称C．的对称中心为D．的图象关于对称【巩固练习2】（2023上·湖南长沙·高一长沙一中校考）我们知道，函数yfx的图象关于坐标原点成中心对称图形的充要条件是函数yfx为奇函数，有同学发现可以将其推广为：函数yfx的图象关于点(,)Pab成中心对称图形的充要条件是函数yfxab为奇函数．（1）请你利用这个结论求得函数323fxxx的对称中心为．（2）已知函数32231xgxxxx与一次函数13ykx有两个交点11,Mxy，22,Nxy，则1122xyxy．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【题...