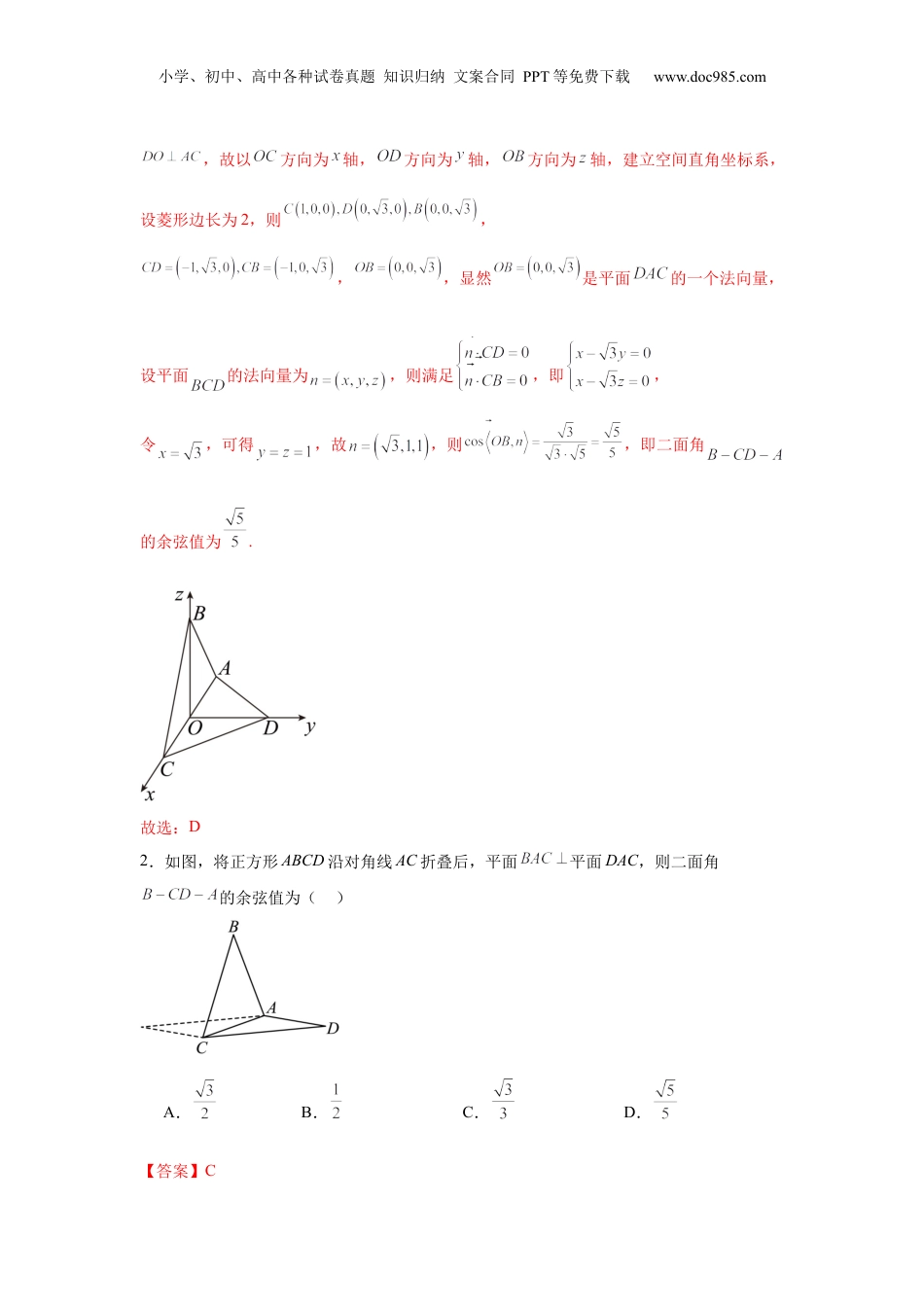
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题突破卷17立体几何中的折叠和探索性问题题型一：两个平面折叠后有关二面角的考察1．已知菱形中，，沿对角线AC折叠之后，使得平面平面，则二面角的余弦值为（）A．2B．C．D．【答案】D【分析】采用建系法，设中点为，以方向为轴，方向为轴，方向为轴，建立空间直角坐标系，分别求出平面和平面的法向量，由向量夹角的余弦公式即可求解.【详解】因为平面平面，设中点为，，则平面，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，故以方向为轴，方向为轴，方向为轴，建立空间直角坐标系，设菱形边长为2，则，，，显然是平面的一个法向量，设平面的法向量为，则满足，即，令，可得，故，则，即二面角的余弦值为.故选：D2．如图，将正方形ABCD沿对角线AC折叠后，平面平面DAC，则二面角的余弦值为（）A．B．C．D．【答案】C小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】根据给定条件，作出二面角的平面角，再在直角三角形中计算作答.【详解】设正方形的边长为a，取AC的中点O，连接BO，则，过O作AD的平行线OE交CD于E，连接BE，如图，因为平面平面DAC，平面平面，平面，则平面DAC，而平面DAC，于是，又，平面BOE，则平面BOE，而平面BOE，即有，因此为二面角的平面角，显然，，有，即为直角三角形，有，则，所以.故选：C3．已知矩形中，，折叠使点A，C重合，折痕为，打开平面，使二面角的大小为，则直线与直线的距离为（）A．B．C．1D．【答案】B【分析】设的中点为P，的中点为Q，则为与的公垂线段，利用题设中的二面角可求公垂线段的长度.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【详解】如图，设的中点为P，则折叠后二面角的平面角为．又，于是是边长为的正三角形．设的中点为Q，则为与的公垂线段，也即直线与直线的距离，为．故选：B.4．如图，已知梯形，．，沿着对角线折叠使得点B，点C的距离为，此时二面角的平面角为（）A．B．C．D．【答案】D【分析】首先分别过作，垂直，交于，根据梯形为等腰梯形得到，从而得到，即可用勾股逆定理证明，根据，即可得到，从而得到平面，即平面平面，从小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com而得到二面角的平面角为.【详解】分别过作，垂直，交于，如图所示：因为，，所以梯形为等腰梯形，则，.在中，，，则.所以，则，即.沿着对角线折叠使得点B，点C的距离为，如图所示：在中，，，则，即.所以平面.又因为平面，所以平面平面，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com即二面角的平面角为.故选：D5．在中，是斜边的高线，现将沿折起，使平面平面，则折叠后的长度为（）A．2B．C．D．3【答案】C【分析】由题意画出平面图及其翻折后的立体图，利用面面垂直的性质可得面，由线面垂直的性质有，进而在直角三角形中应用勾股定理求.【详解】由题设，可得如下平面图及其翻折后的立体图，，∴，，又面面，面面，，面，∴面，而面，故，∴在中，.故选：C.6．，是直线上的两点，若沿轴将坐标平面折成的二面角，则折叠后、两点间的距离是（）A．6B．C．D．【答案】A小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】作轴于点，作轴于点，将用表示，再根据数量积的运算律结合向量的模的计算公式计算即可.【详解】因为，是直线上的两点，所以，，如图为折叠后的图形，作轴于点，作轴于点，则异面直线，所成的角为，即、的夹角为，，，，，则，即折叠后、两点间的距离为.故选：A.7．在矩形ABCD中，，M是AD边上一点，将矩形ABCD沿BM折叠，使平面与平面互相垂直，则折叠后A，C两点之间距离的最小值是（）A．B．C．D．【答案】D【分析】根据立体几何中面面垂直的相关性质以及余弦定理、正弦二倍角公式运算求解即可.【详解】作示意图如下，在平面中，作，连接，因为平面平面，平面平面，，平面小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，所以平...