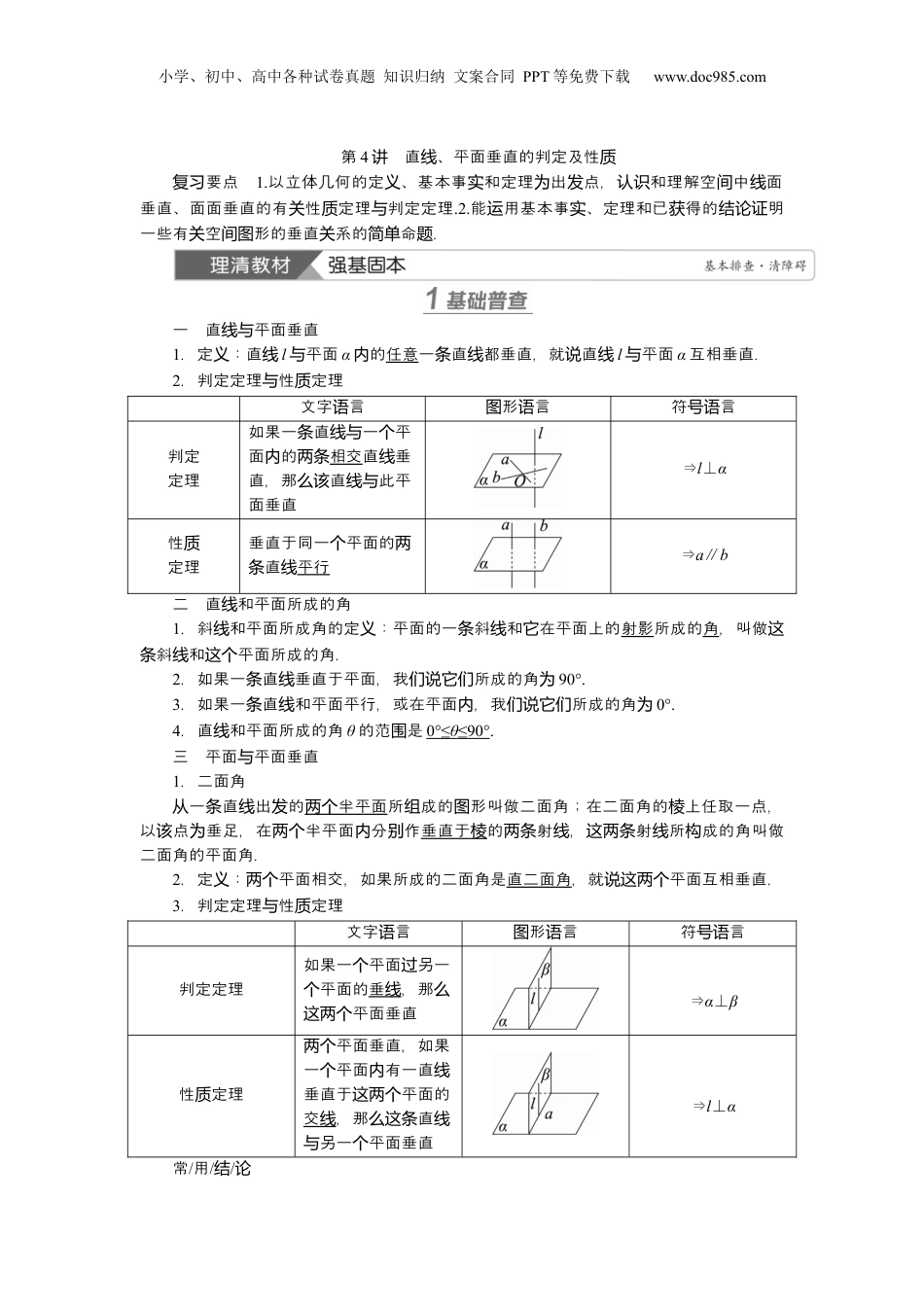
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第4直、平面垂直的判定及性讲线质要点复习1.以立体几何的定、基本事和定理出点，和理解空中面义实为发认识间线垂直、面面垂直的有性定理判定定理关质与.2.能用基本事、定理和已得的明运实获结论证一些有空形的垂直系的命．关间图关简单题一直平面垂直线与1．定：直义线l平面与α的内任意一直都垂直，就直条线说线l平面与α互相垂直．2．判定定理性定理与质文字言语形言图语符言号语判定定理如果一直一平条线与个面的内两条相交直垂线直，那直此平么该线与面垂直⇒l⊥α性质定理垂直于同一平面的个两直条线平行⇒a∥b二直和平面所成的角线1．斜和平面所成角的定：平面的一斜和在平面上的线义条线它射影所成的角，叫做这斜和平面所成的角．条线这个2．如果一直垂直于平面，我所成的角条线们说它们为90°.3．如果一直和平面平行，或在平面，我所成的角条线内们说它们为0°.4．直和平面所成的角线θ的范是围0°≤θ≤90°.三平面平面垂直与1．二面角一直出的从条线发半平面两个所成的形叫做二面角；在二面角的上任取一点，组图棱以点垂足，在半平面分作该为两个内别垂直于棱的射，射所成的角叫做两条线这两条线构二面角的平面角．2．定：平面相交，如果所成的二面角是义两个直二面角，就平面互相垂直．说这两个3．判定定理性定理与质文字言语形言图语符言号语判定定理如果一平面另一个过平面的个垂线，那么平面垂直这两个⇒α⊥β性定理质平面垂直，如果两个一平面有一直个内线垂直于平面的这两个交线，那直么这条线另一平面垂直与个⇒l⊥α常/用/结/论小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1．若平行中的一直垂直于一平面，另一直也垂直于平面．两条线条线个则条线这个2．垂直于同一直的平面平行．条线两个3．一直垂直于平行平面中的一，直另一平面也垂直．条线两个则这条线与个4．相交平面同垂直于第三平面，的交也垂直于第三平面．两个时个它们线个1．判下列是否正确．断结论(1)“直线l垂直于平面α的无直”是“内数条线l⊥α”的必要不充分件．条(√)(2)垂直于同一平面的平面平行．个两()(3)若平面垂直，其中一平面的任意一直垂直于另一平面．两则个内条线个()(4)若直线a⊥平面α，直线b⊥平面α，直则线a∥直线b.(√)(5)若平面α⊥平面β，直线a⊥平面β，则a∥α.()2．(材改教编)在三棱锥PABC中，点P在平面ABC中的射影点为O.(1)若PA＝PB＝PC，点则O是△ABC的________心；(2)若PA⊥PB，PB⊥PC，PC⊥PA，点则O是△ABC的________心．答案：(1)外(2)垂3．(2024·福建泉州模拟)已知平面α⊥平面β，直线m⊂平面α，直线n⊂平面β，α∩β＝l，出下列法：给说①若m⊥n，则m⊥l；②若m⊥l，则m⊥β；③若m⊥β，则m⊥n，其中正确法的序说号为()A．①②③B．①②C．①③D．②③解析：平面α⊥平面β，直线m⊂平面α，直线n⊂平面β，α∩β＝l，①若m⊥n，可得m，l可能平行，故①；错误②若m⊥l，由面面垂直的性定理可得质m⊥β，故②正确；③若m⊥β，可得m⊥n，故③正确．故选D.答案：D4．(多选)如，图PA垂直于以AB直的所在的平面，为径圆C上于为圆异A，B的任意一点，AE⊥PC，垂足为E，点F是PB上一点，下列判中正确的是则断()A．BC⊥平面PACB．AE⊥EFC．AC⊥PBD．平面AEF⊥平面PBC解析：于对A，PA垂直于以AB直的所在的平面，而为径圆BC⊂底面面，圆则PA⊥BC，又由的性可知圆质AC⊥BC，且PA∩AC＝A，PA，AC⊂平面PAC，则BC⊥平面PAC，所以A正确；于对B，由A可知项BC⊥AE，由意可知题AE⊥PC，且BC∩PC＝C，BC，PC⊂平面PBC，所以AE⊥平面PBC，而EF⊂平面PBC，所以AE⊥EF，所以B正确；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com于对C，由B可知项AE⊥平面PBC，因而AC平面与PBC不垂直，若AC⊥PB，易得则AC⊥平面PBC，矛盾，所以C；于错误对D，由B可知，项AE⊥平面PBC，AE⊂平面AEF，由面面垂直的判定定理可得平面AEF⊥平面PBC，所以D正确．故选ABD.答案：ABD型题垂直面垂直线线与线典例1(2024·福建三明模拟)如所示，在三柱图棱ABCA1B1C1...