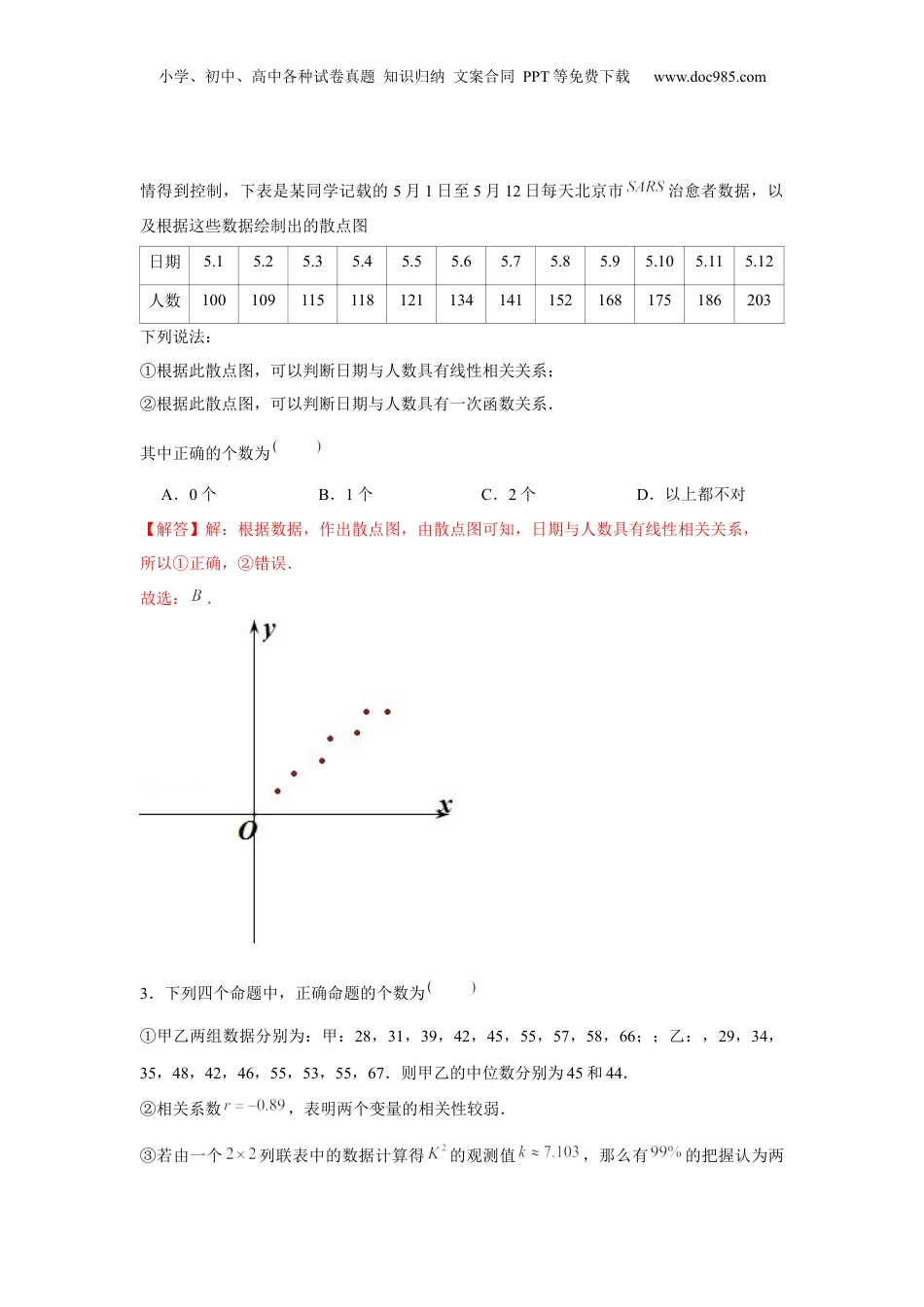
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com跟踪训练07成对数据的统计分析一．选择题（共15小题）1．一组成对数据，，，，，，，，样本中心点为，由这组数据拟合的线性回归方程为，用最小二乘法求回归方程是为了使最小．A．总偏差平方和B．残差平方和C．回归平方和D．竖直距离和【解答】解：一组成对数据，，，，，，，，，由这组数据拟合的线性回归方程为，用最小二乘法求回归方程是为了使残差平方和最小．故选：．2．2003年春季，我国部分地区流行，党和政府采取果断措施，防治结合，很快使病小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com情得到控制，下表是某同学记载的5月1日至5月12日每天北京市治愈者数据，以及根据这些数据绘制出的散点图日期5.15.25.35.45.55.65.75.85.95.105.115.12人数100109115118121134141152168175186203下列说法：①根据此散点图，可以判断日期与人数具有线性相关关系；②根据此散点图，可以判断日期与人数具有一次函数关系．其中正确的个数为A．0个B．1个C．2个D．以上都不对【解答】解：根据数据，作出散点图，由散点图可知，日期与人数具有线性相关关系，所以①正确，②错误．故选：．3．下列四个命题中，正确命题的个数为①甲乙两组数据分别为：甲：28，31，39，42，45，55，57，58，66；；乙：，29，34，35，48，42，46，55，53，55，67．则甲乙的中位数分别为45和44．②相关系数，表明两个变量的相关性较弱．③若由一个列联表中的数据计算得的观测值，那么有的把握认为两小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com个变量有关．④用最小二乘法求出一组数据，，，，的回归直线方程后要进行残差分析，相应于数据，，，，的残差是指．0.100.050.0250.0100.0050.0012.7063.8415.0246.6357.87910.828A．1B．2C．3D．4【解答】解：对于①，甲组数据的中位数为45，乙组数据的中位数为，①错误；对于②，相关系数时，两个变量有很强的相关性，②错误；对于③，的观测值约为，那么有的把握认为两个变量有关，③正确；对于④，残差分析中，相应数据，，，2，，的残差，④正确；所以命题正确的序号是③④．故选：．4．下列命题错误的是A．在回归分析模型中，残差平方和越大，说明模型的拟合效果越好B．线性相关系数越大，两个变量的线性相关性越强；反之，线性相关性越弱C．由变量和的数据得到其回归直线方程，则一定经过，D．在回归直线方程中，当解释变量每增加一个单位时，预报变量增加0.1个单位．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解答】解：比较两个模型的拟合效果，可以比较残差平方和的大小，残差平方和越小的模型，拟合效果越好，故错误；线性相关系数越大，两个变量的线性相关性越强；反之，线性相关性越弱，正确；回归直线方程，则一定经过，，正确；在回归直线方程中，当解释变量每增加一个单位时，预报变量增加0.1个单位，正确．故选：．5．2020年初，新型冠状病毒引起的肺炎疫情暴发以来，各地医疗机构采取了各种针对性的治疗方法，取得了不错的成效，某地开始使用中西医结合方法后，每周治愈的患者人数如表所示：周数12345治愈人数2173693142由表格可得关于的二次回归方程为，则此回归模型第2周的残差（实际值与预报值之差）为A．5B．4C．1D．0【解答】解：设，则，，，所以，令，得．故选：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com6．已知一组样本点，其中，2，3，，30，根据最小二乘法求得的回归直线方程是，则下列说法正确的是A．若所有样本点都在回归直线上，则变量间的相关系数为1B．至少有一个样本点落在回归直线上C．变量，之间的线性相关程度越强，其相关系数越接近1D．若的斜率，则变量与正相关【解答】解：选项，若所有样本点都在回归直线上，则变量间的相关系数的绝对值为1，相关系数，故错误；选项，回归直线必过样本点的中心，但样本点可能都不在回归直线上，故错误；选项，随机变量之间的线性相关程度越强，越接近1，故错误；选项，相关系数与符号相...