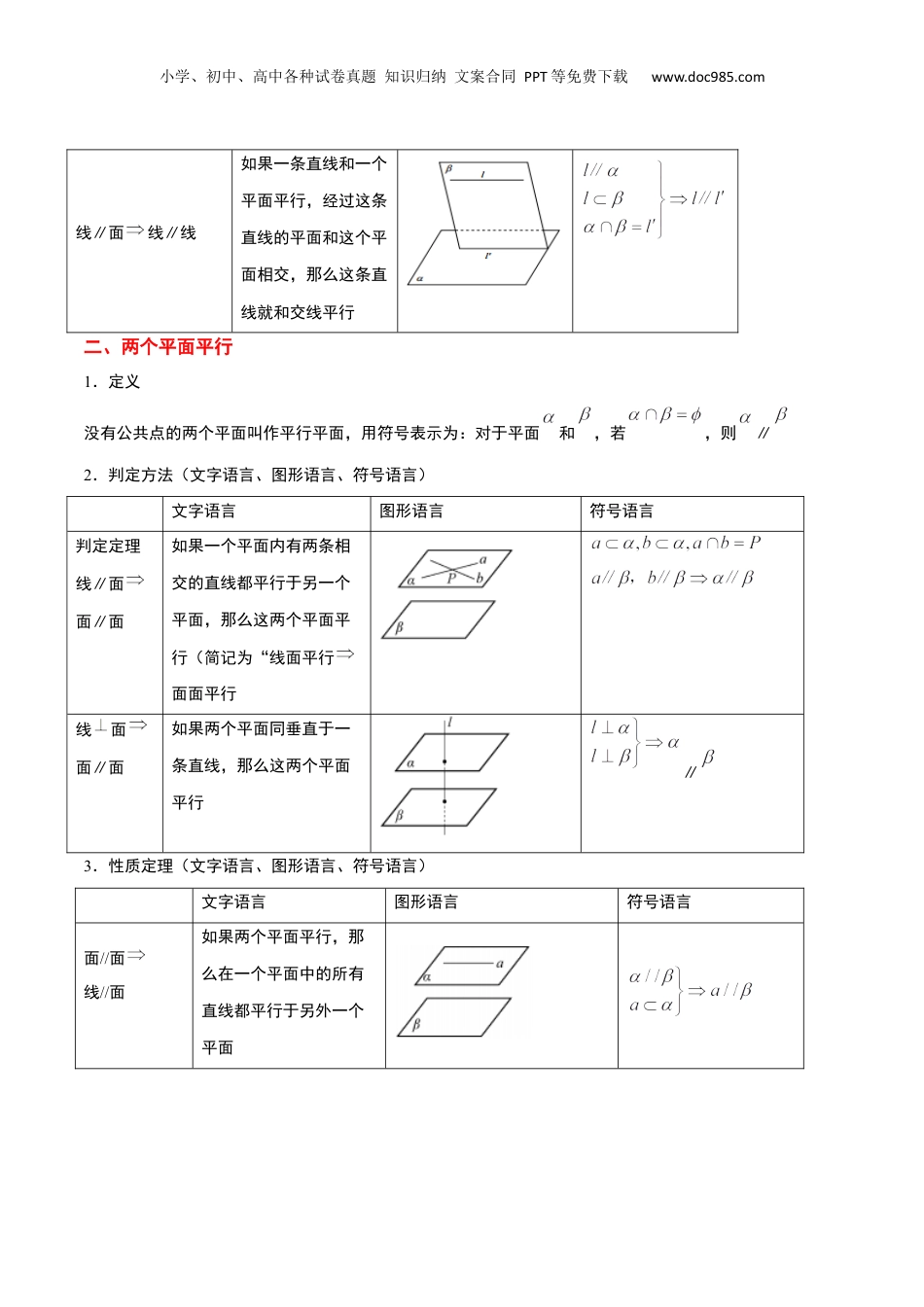
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）第33讲空间直线、平面的平行（精讲）题型目录一览①线面平行Ⅰ—利用三角形中位线②线面平行Ⅱ—利用平行四边形③线面平行Ⅲ—利用线面平行的性质定理④线面平行Ⅳ—利用面面平行⑤面面平行的判定定理一、直线和平面平行1．定义直线与平面没有公共点，则称此直线与平面平行，记作∥2．判定方法（文字语言、图形语言、符号语言）文字语言图形语言符号语言线∥线线∥面如果平面外的一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行（简记为“线线平行线面平行面∥面线∥面如果两个平面平行，那么在一个平面内的所有直线都平行于另一个平面3．性质定理（文字语言、图形语言、符号语言）文字语言图形语言符号语言一、知识点梳理小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com线∥面线∥线如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行二、两个平面平行1．定义没有公共点的两个平面叫作平行平面，用符号表示为：对于平面和，若，则∥2．判定方法（文字语言、图形语言、符号语言）文字语言图形语言符号语言判定定理线∥面面∥面如果一个平面内有两条相交的直线都平行于另一个平面，那么这两个平面平行（简记为“线面平行面面平行线面面∥面如果两个平面同垂直于一条直线，那么这两个平面平行∥3．性质定理（文字语言、图形语言、符号语言）文字语言图形语言符号语言面//面线//面如果两个平面平行，那么在一个平面中的所有直线都平行于另外一个平面小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com性质定理如果两个平行平面同时和第三个平面相交，那么他们的交线平行（简记为“面面平行线面平行”）面//面线面如果两个平面中有一个垂直于一条直线，那么另一个平面也垂直于这条直线【常用结论】1.证明直线与平面平行的常用方法：①利用定义，证明直线与平面没有公共点，一般结合反证法证明；②利用线面平行的判定定理，即线线平行线面平行．辅助线的作法为：平面外直线的端点进平面，同向进面，得平行四边形的对边，不同向进面，延长交于一点得平行于第三边的线段；③利用面面平行的性质定理，把面面平行转化成线面平行；2.证明面面平行的常用方法：①利用面面平行的定义，此法一般与反证法结合；②利用面面平行的判定定理；③利用两个平面垂直于同一条直线；④证明两个平面同时平行于第三个平面．3.证明线线平行的常用方法：①利用直线和平面平行的判定定理；②利用平行公理；题型一线面平行Ⅰ—利用三角形中位线策略方法1.可以拿一把直尺放在位置（与平），如一；齐图2.然后把直尺平行往平面方向移，直到直尺第一次落在平面动停止，如二；内图二、题型分类精讲小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3.此好点时刚经过（里熟后可以直接凭感直接找到点这练数），此直尺所在的位置就时是我要找的平行，直尺们线与相交于点，接连，如三；图4.此时度有有短，接长长连延好交于一点并长刚，好成刚构型模型（为中点，则也为中点，若等分点，为则也为等分点），对应，如图四．1234012340BCADPPDACBEEF图一图二图三图四【典例1】如图，垂直于梯形所在平面，，为的中点，，，四边形为矩形.求证：平面；【答案】证明见解析【分析】可先由中位线证明两线平行，再证明线面平行.【详解】令交于,连接,PDACBEFFBCADPE小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com四边形为矩形，为中点，又为的中点，，又平面，平面.平面【题型训练】一、解答题1．（2023·全国·高三专题练习）在如图所示的三棱锥中，已知为的中点，为的中点，为的中点.证明：平面.【答案】证明见解析【分析】利用线面平行判定定理即可证得平面.【详解】因为是的中位线，所以.因为平面平面，所以平面.2．（2023·全国·高三专题练习）如图，在四棱锥中，底面为矩形，为中点，证明：平面小学、初中、高...