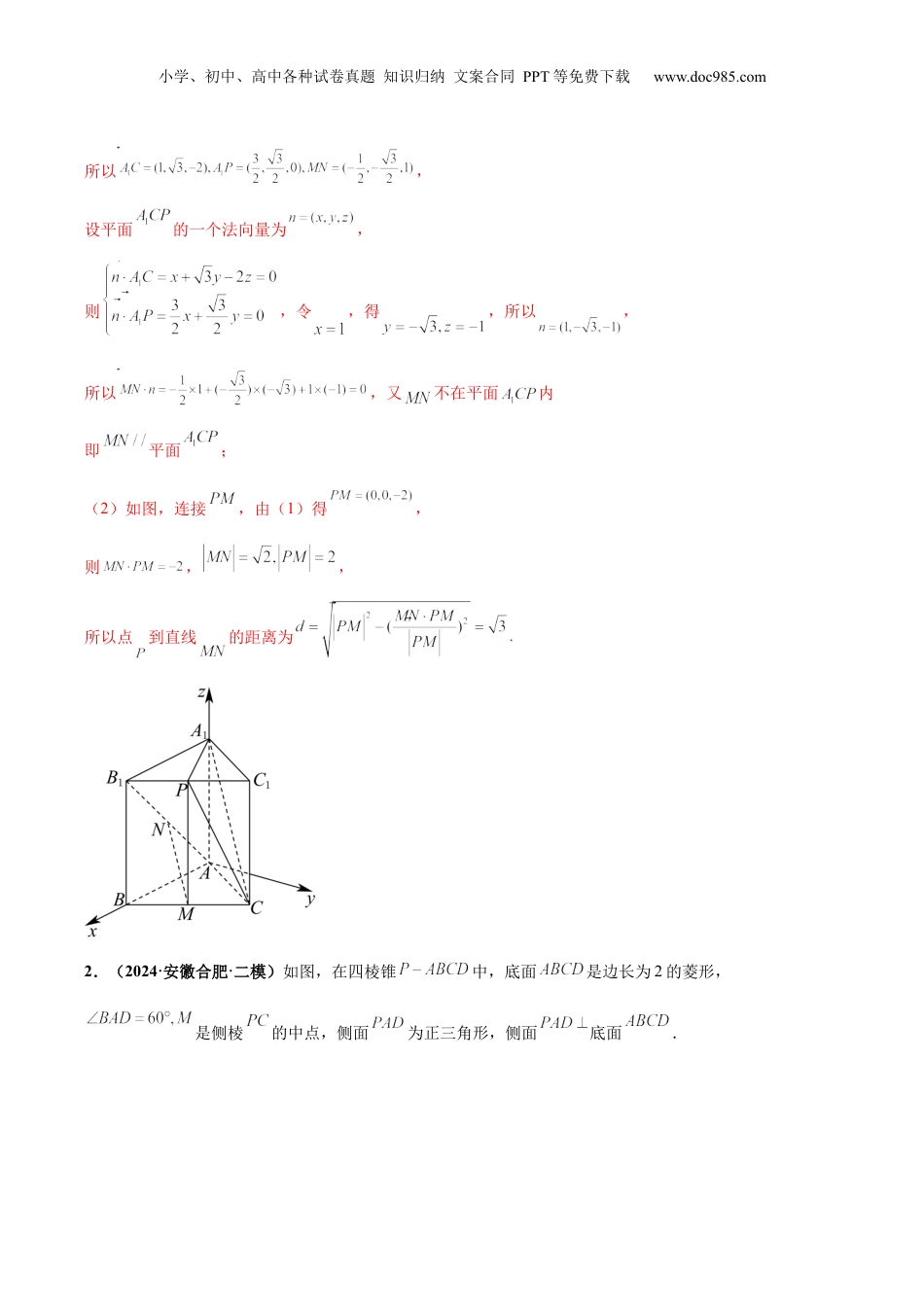
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com黄金冲刺大题03立体几何1．（2024·黑龙江·二模）如图，已知正三棱柱的侧棱长和底面边长均为2，M是BC的中点，N是的中点，P是的中点．(1)证明：平面；(2)求点P到直线MN的距离．【答案】(1)证明见解析(2)【分析】（1）建立如图空间直角坐标系，设平面的一个法向量为，利用空间向量法证明即可；（2）利用空间向量法即可求解点线距.【详解】（1）由题意知，平面，，而平面，所以，在平面内过点A作y轴，使得y轴，建立如图空间直角坐标系，则，得，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以，设平面的一个法向量为，则，令，得，所以，所以，又不在平面内即平面；（2）如图，连接，由（1）得，则，，所以点到直线的距离为.2．（2024·安徽合肥·二模）如图，在四棱锥中，底面是边长为2的菱形，是侧棱的中点，侧面为正三角形，侧面底面．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)求三棱锥的体积；(2)求与平面所成角的正弦值．【答案】(1)(2)．【分析】（1）作出辅助线，得到线线垂直，进而得到线面垂直，由中位线得到到平面的距离为，进而由锥体体积公式求出答案；（2）证明出，建立空间直角坐标系，求出平面的法向量，进而由法向量的夹角余弦值的绝对值求出线面角的正弦值.【详解】（1）如图所示，取的中点，连接．因为是正三角形，所以．又因为平面底面平面，平面平面，所以平面，且．又因为是的中点，到平面的距离为，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，所以三棱锥的体积为．（2）连接，因为，所以为等边三角形，所以，以为原点，所在直线分别为轴，轴，轴，建立如图所示的空间直角坐标系，则，所以．设平面的法向量为，则，即，解得，取，则，所以．设与平面所成角为，则．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com即与平面所成角的正弦值为．3．（2023·福建福州·模拟预测）如图，在三棱柱中，平面平面，．(1)设为中点，证明：平面；(2)求平面与平面夹角的余弦值．【答案】(1)证明见解析；(2)【分析】（1）根据等边三角形的性质得出，根据平面平面得出平面，，利用勾股定理得出，从而证明平面；（2）建立空间直角坐标系，利用坐标表示向量，求出平面的法向量和平面的一个法向量，利用向量求平面与平面的夹角余弦值．【详解】（1）证明：因为为中点，且，所以在中，有，且，又平面平面，且平面平面，平面,小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以平面，又平面，则，由，，得，因为，，，所以由勾股定理，得，又，平面，所以平面；（2）如图所示，以为原点，建立空间直角坐标系，可得，则，设平面的法向量为，由，令，得，，所以,由（1）知，平面，所以平面的一个法向量为，记平面与平面的夹角为，则，所以平面与平面夹角的余弦值为．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4．（2024·山西晋中·三模）如图，在六面体中，，，且，平行于平面，平行于平面，.(1)证明：平面平面；(2)若点到直线的距离为，为棱的中点，求平面与平面夹角的余弦值．【答案】(1)证明见解析(2)【分析】（1）设平面与直线交于点，使用线面平行的性质，然后用面面垂直的判定定理即可；（2）证明平面，然后构造空间直角坐标系，直接用空间向量方法即可得出结果.【详解】（1）设平面与直线交于点，连接，则平面与平面的交线为，平面与平面的交线为，因为平行于平面，平面，平面和平面的交线为，所以．同理，所以四边形是平行四边形，故，.因为，，所以，又，所以为棱的中点在中，，，所以，由于，故.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com而，，平面，所以平面，又平面，所以平面平面（2）由（1）可知，平面，又平面，所以.而点到直线的距离为，故.在等腰直角三角形中，由得在等腰三角形中，由，，得.在平行四边形中，，，，由余弦定理得，所以，所以.因为，所以.因为...