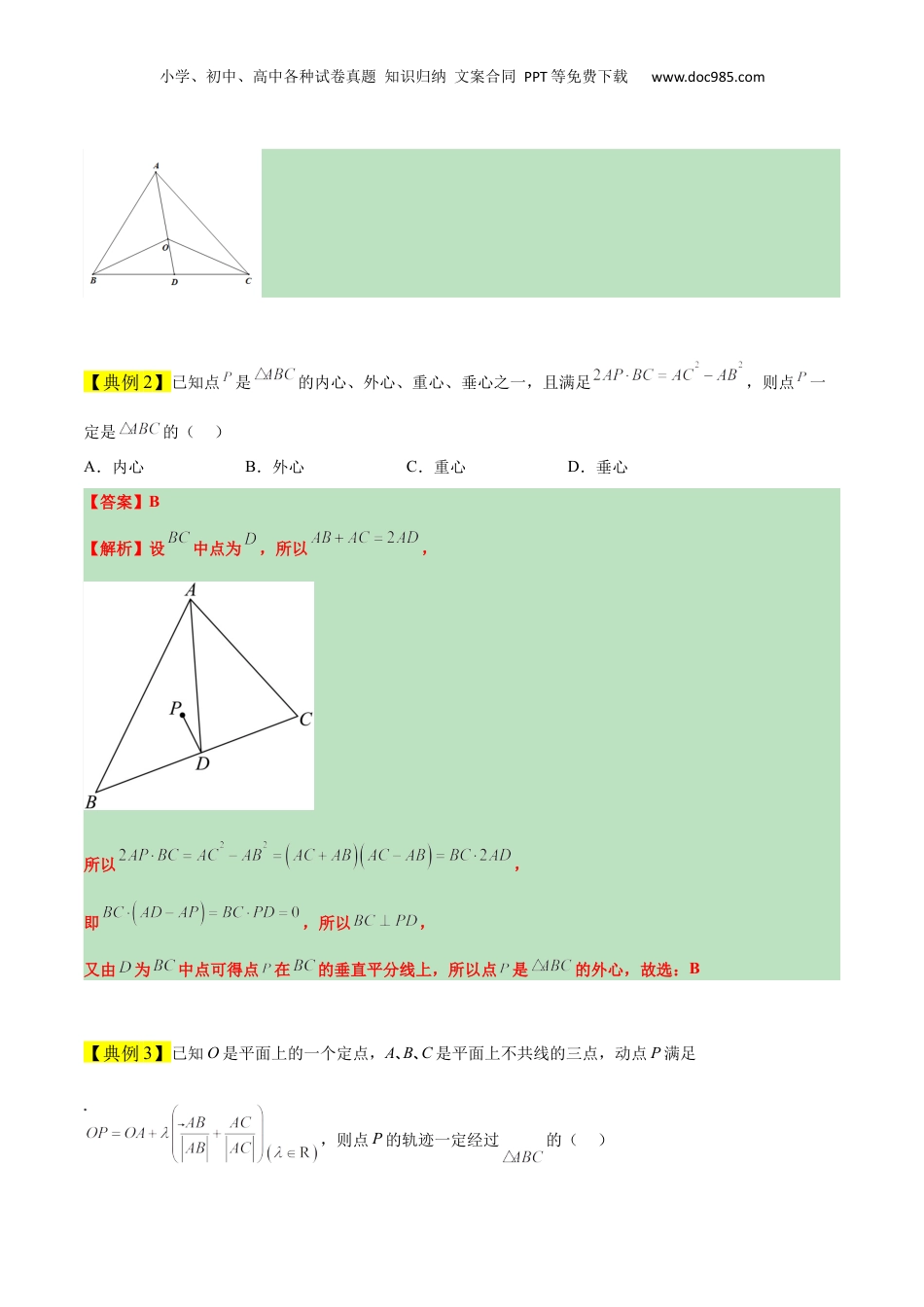
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）素养拓展13三角形中的“四心”问题（精讲+精练）一、三角形的四心定义外心：三角形三边的垂直平分线的交点为三角形的外心，外心到三个顶点的距离相等；内心：三角形三个角的角平分线的交点为三角形的内心，内心到三边的距离相等；重心：三角形三条中线的交点为三角形的重心，重心为中线的三等分点；垂心：三角形三边上的高或其延长线的交点为三角形的垂心；二、三角形的重心（1）三角形的重心是三角形三边中线的交点．（2）重心的性质：①重心到顶点的距离与重心到对边中点的距离之比为2：1．②重心和三角形3个顶点组成的3个三角形面积相等．重要结论：（1）设点是△所在平面内的一点，则当点是△的重心时，有或（其中为平面内任意一点）；（2）在向量的坐标表示中，若、、、分别是三角形的重心和三个顶点，且分别为、、，，则有.三、三角形的外接圆与外心（1）外接圆：经过三角形的三个顶点的圆，叫做三角形的外接圆．（2）外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心．注：①“接”是说明三角形的顶点在圆上，或者经过三角形的三个顶点．②锐角三角形的外心在三角形的内部；直角三角形的外心为直角三角形斜边的中点；钝角三角形的外心在三角形的外部．③找一个三角形的外心，就是找一个三角形的三条边的垂直平分线的交点，三角形的外接圆只有一个，而一、知识点梳理小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com一个圆的内接三角形却有无数个．重要结论：若点是△的外心，则或；反之，若或，则点是△的外心。四、三角形的内切圆与内心（1）内切圆的有关概念：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．（2）三角形内心的性质：三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．重要结论：若点是△的内心，则有；反之，若，则点是△的内心．五、垂心三角形三边上的高或其延长线的交点为三角形的垂心.重要结论：若是△的垂心，则或，反之，若HAHCHCHBHBHA或，则是△的垂心．【典例1】若为的重心（重心为三条中线交点），且，则___．【答案】【解析】在中，取中点，连接，由重心的性质可得为的三等分点，且，又为的中点，所以，所以，所以.故答案为：二、题型精讲精练小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【典例2】已知点是的内心、外心、重心、垂心之一，且满足，则点一定是的（）A．内心B．外心C．重心D．垂心【答案】B【解析】设中点为，所以，所以，即，所以，又由为中点可得点在的垂直平分线上，所以点是的外心，故选：B【典例3】已知O是平面上的一个定点，A､B､C是平面上不共线的三点，动点P满足，则点P的轨迹一定经过的（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．重心B．外心C．内心D．垂心【答案】C【解析】因为为方向上的单位向量，为方向上的单位向量，则的方向与的角平分线一致，由，可得，即，所以点P的轨迹为的角平分线所在直线，故点P的轨迹一定经过的内心.故选：C.【典例4】设为的外心，若，则是的（）A．重心（三条中线交点）B．内心（三条角平分线交点）C．垂心（三条高线交点）D．外心（三边中垂线交点）【答案】C【解析】在中，为外心，可得， ，∴，设的中点为，则，，∴，可得在边的高线上．同理可证，在边的高线上，故是三角形两高线的交点，可得是三角形的垂心，故选：C【题型训练-刷模拟】小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1.重心一、单选题1．（四川省泸州市泸县第五中学2023届高三下学期二诊模拟考试文科数学试题）已知△ABC的重心为O，则向量（）A．B．C．D．2．（2023·全国·高三专题练习）O是平面内一定点，A，B，C是平面内不共线三点，动点P满...