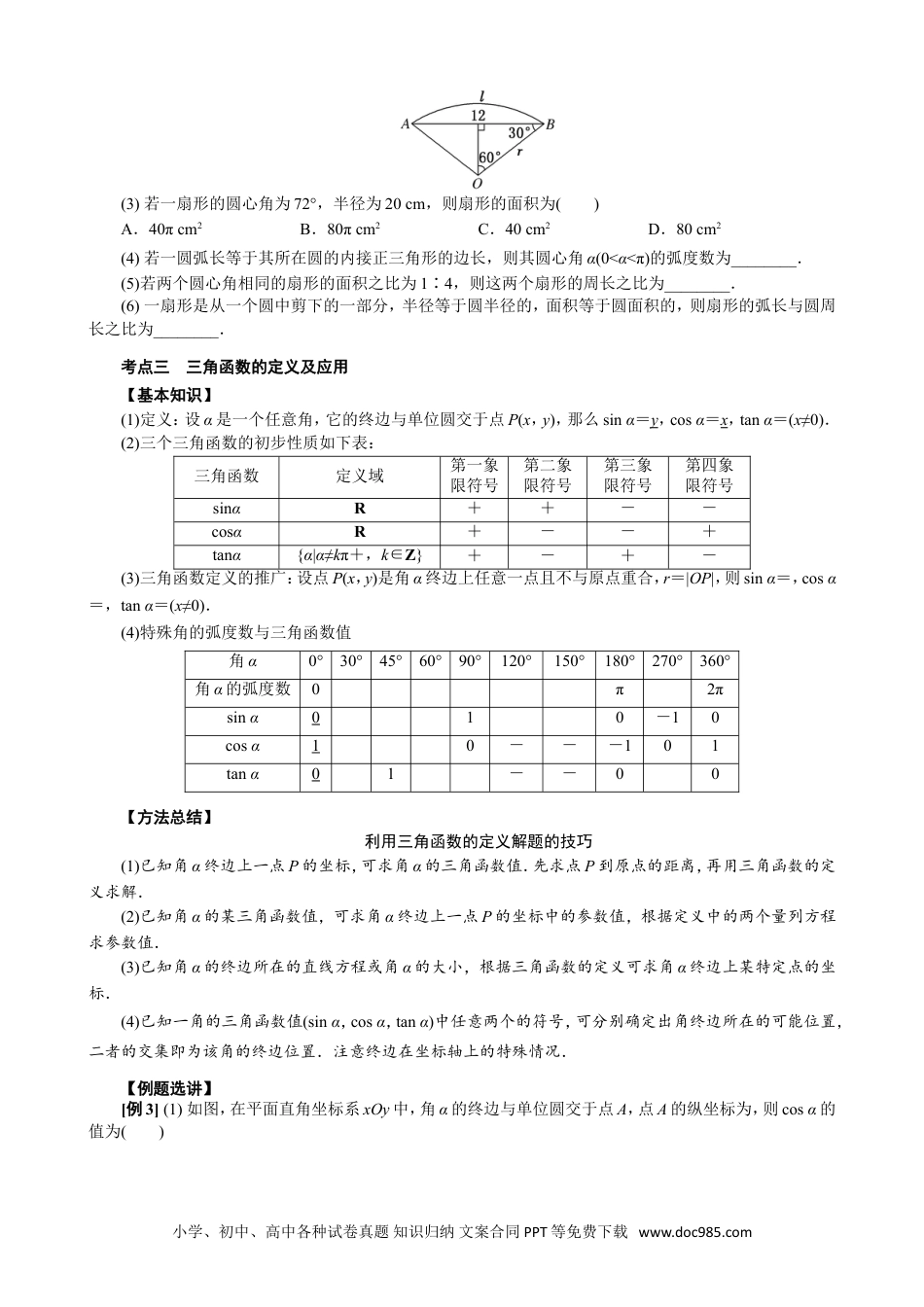
专题一任意角、弧度制及任意角的三角函数考点一角的概念【基本知识】(1)定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．(2)角的分类(3)终边相同的角：所有与角α终边相同的角，连同角α在内，构成的角的集合是S＝{β|β＝k·360°＋α，k∈Z}．【例题选讲】[例1](1)集合中的角所表示的范围(阴影部分)是()(2)若角α是第二象限角，则是()A．第一象限角B．第二象限角C．第一或第三象限角D．第二或第四象限角(3)给出下列四个命题：①－是第二象限角；②是第三象限角；③－400°是第四象限角；④－315°是第一象限角．其中正确的命题有()A．1个B．2个C．3个D．4个(4)已知点P(cosα，tanα)在第三象限，则角α的终边在()A．第一象限B．第二象限C．第三象限D．第四象限(5)在－720°～0°范围内所有与45°终边相同的角为________．(6)终边在直线y＝x上的角的集合为_________________________．考点二扇形的弧长及面积公式的应用【基本知识】(1)弧度制定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，用符号rad表示，读作弧度．正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是0．(2)角度制和弧度制的互化：180°＝πrad，1°＝rad，1rad＝°．(3)扇形的弧长公式：l＝|α|·r，扇形的面积公式：S＝lr＝|α|·r2．【例题选讲】[例2](1)已知扇形的周长是6，面积是2，则扇形的圆心角的弧度数是()A．1B．4C．1或4D．2或4(2)若扇形的圆心角是α＝120°，弦长AB＝12cm，则弧长l＝________cm．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(3)若一扇形的圆心角为72°，半径为20cm，则扇形的面积为()A．40πcm2B．80πcm2C．40cm2D．80cm2(4)若一圆弧长等于其所在圆的内接正三角形的边长，则其圆心角α(0<α<π)的弧度数为________．(5)若两个圆心角相同的扇形的面积之比为1∶4，则这两个扇形的周长之比为________．(6)一扇形是从一个圆中剪下的一部分，半径等于圆半径的，面积等于圆面积的，则扇形的弧长与圆周长之比为________．考点三三角函数的定义及应用【基本知识】(1)定义：设α是一个任意角，它的终边与单位圆交于点P(x，y)，那么sinα＝y，cosα＝x，tanα＝(x≠0)．(2)三个三角函数的初步性质如下表：三角函数定义域第一象限符号第二象限符号第三象限符号第四象限符号sinαR＋＋－－cosαR＋－－＋tanα{α|α≠kπ＋，k∈Z}＋－＋－(3)三角函数定义的推广：设点P(x，y)是角α终边上任意一点且不与原点重合，r＝|OP|，则sinα＝，cosα＝，tanα＝(x≠0)．(4)特殊角的弧度数与三角函数值角α0°30°45°60°90°120°150°180°270°360°角α的弧度数0π2πsinα010－10cosα10－－－101tanα01－－00【方法总结】利用三角函数的定义解题的技巧(1)已知角α终边上一点P的坐标，可求角α的三角函数值．先求点P到原点的距离，再用三角函数的定义求解．(2)已知角α的某三角函数值，可求角α终边上一点P的坐标中的参数值，根据定义中的两个量列方程求参数值．(3)已知角α的终边所在的直线方程或角α的大小，根据三角函数的定义可求角α终边上某特定点的坐标．(4)已知一角的三角函数值(sinα，cosα，tanα)中任意两个的符号，可分别确定出角终边所在的可能位置，二者的交集即为该角的终边位置．注意终边在坐标轴上的特殊情况．【例题选讲】[例3](1)如图，在平面直角坐标系xOy中，角α的终边与单位圆交于点A，点A的纵坐标为，则cosα的值为()小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．－C．D．－(2)设α是第二象限角，P(x，4)为其终边上的一点，且cosα＝x，则tanα＝()A．B．C．－D．－(3)已知角θ的顶点与原点重合，始边与x轴的非负半轴重合，终边在直线y＝2x上，则cos2θ＝()A．－B．－C．D．(4)已知A(xA，yA)是单位圆(圆心在坐标原点O)上任意一点，将射线OA绕O点逆时针旋转30°，交单位圆于点B(xB，yB)，则xA－yB的取值范围是()A．[－2，2]B．[－，]C．[－1，1]D．(5)若sinαtanα<0，且<0，则角α是()A．第一象限角B．第二象限角C．第三象限角D．第四象限角(6)s...