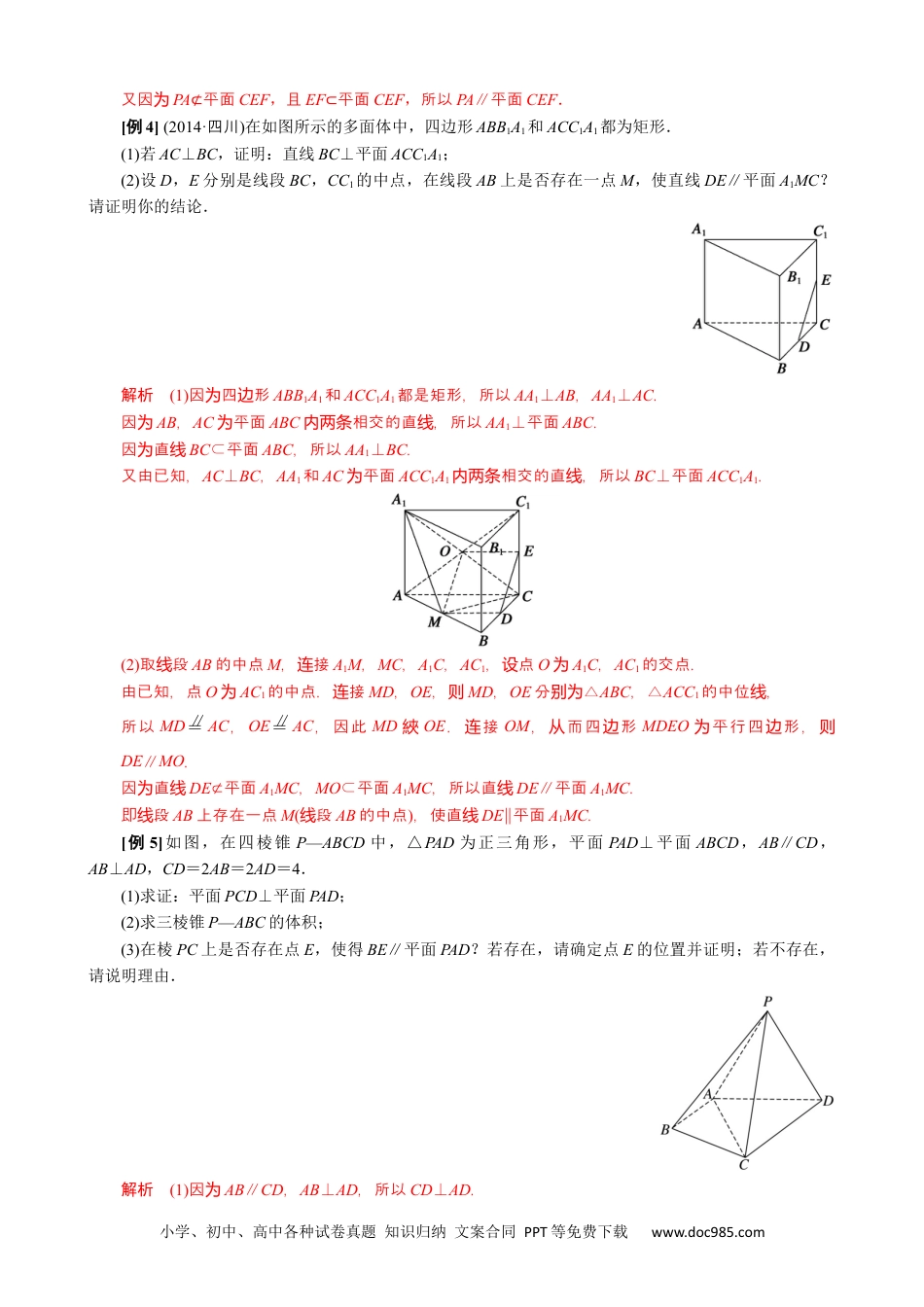
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题09立体几何中的探索性问题【方法总结】解决立体几何中的探索性问题的途径解探索性一般先假求解的果存在，果出，找使成立的充分件，决问题设结从这个结发寻这个结论条如果找到了使成立的充分件，存在；如果找不到使成立的充分件结论条则结论条(出矛盾现)，不存在．则而于探求点的，一般是先探求点的位置，多段的中点或某三等分点，然后出符合要求的对问题为线个给明．证考点一探究平行问题【例题选讲】[例1](2018·全国Ⅲ)如图，矩形ABCD所在平面与半圆弧所在平面垂直，M是上异于C，D的点．(1)证明：平面AMD⊥平面BMC．(2)在线段AM上是否存在点P，使得MC∥平面PBD？说明理由．解析(1)由知，平面题设CMD⊥平面ABCD，交线为CD．因为BC⊥CD，BC⊂平面ABCD，所以BC⊥平面CMD，所以BC⊥DM．因为M为上于异C，D的点，且DC直，所以为径DM⊥CM．又BC∩CM＝C，所以DM⊥平面BMC．因为DM⊂平面AMD，所以平面AMD⊥平面BMC．(2)当P为AM的中点时，MC∥平面PBD．明如下：证接连AC交BD于O．因四形为边ABCD矩形，所以为O为AC的中点．接连OP，因为P为AM的中点，所以MC∥OP．又MC⊄平面PBD，OP⊂平面PBD，所以MC∥平面PBD．[例2](2019·北京)如图，在四棱锥P－ABCD中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点．(1)求证：BD⊥平面PAC；(2)若∠ABC＝60°，求证：平面PAB⊥平面PAE；(3)棱PB上是否存在点F，使得CF∥平面PAE？说明理由．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com解析(1)因为PA⊥平面ABCD，BD⊂平面ABCD，所以PA⊥BD．因底面为ABCD菱形，所以为BD⊥AC．又PA∩AC＝A，所以BD⊥平面PAC．(2)因为PA⊥平面ABCD，AE⊂平面ABCD，所以PA⊥AE．因底面为ABCD菱形为，∠ABC＝60°，且E为CD的中点，所以AE⊥CD．又因为AB∥CD，所以AB⊥AE．又AB∩PA＝A，所以AE⊥平面PAB．因为AE⊂平面PAE，所以平面PAB⊥平面PAE．(3)棱PB上存在点F，使得CF∥平面PAE．理由如下：取PB的中点F，PA的中点G，接连CF，FG，EG，则FG∥AB，且FG＝AB．因底面为ABCD菱形，且为E为CD的中点，所以CE∥AB，且CE＝AB．所以FG∥CE，且FG＝CE．所以四形边CEGF平行四形．所以为边CF∥EG．因为CF⊄平面PAE，EG⊂平面PAE，所以CF∥平面PAE．[例3](2016·北京)如图，在四棱锥P－ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC．(1)求证：DC⊥平面PAC．(2)求证：平面PAB⊥平面PAC．(3)设点E为AB的中点，在棱PB上是否存在点F，使得PA∥平面CEF？说明理由．解析(1)因为PC⊥平面ABCD，所以PC⊥DC．又因为DC⊥AC，且PC∩AC＝C，所以DC⊥平面PAC．(2)因为AB∥DC，DC⊥AC，所以AB⊥AC．因为PC⊥平面ABCD，所以PC⊥AB．又因为PC∩AC＝C，所以AB⊥平面PAC．又AB⊂平面PAB，所以平面PAB⊥平面PAC．(3)棱PB上存在点F，使得PA∥平面CEF．理由如下：取PB的中点F，接连EF，CE，CF．因为E为AB的中点，所以EF∥PA．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com又因为PA⊄平面CEF，且EF⊂平面CEF，所以PA∥平面CEF．[例4](2014·四川)在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形．(1)若AC⊥BC，证明：直线BC⊥平面ACC1A1；(2)设D，E分别是线段BC，CC1的中点，在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．解析(1)因四形为边ABB1A1和ACC1A1都是矩形，所以AA1⊥AB，AA1⊥AC．因为AB，AC平面为ABC相交的直，所以内两条线AA1⊥平面ABC．因直为线BC⊂平面ABC，所以AA1⊥BC．又由已知，AC⊥BC，AA1和AC平面为ACC1A1相交的直，所以内两条线BC⊥平面ACC1A1．(2)取段线AB的中点M，接连A1M，MC，A1C，AC1，点设O为A1C，AC1的交点．由已知，点O为AC1的中点．接连MD，OE，则MD，OE分别为△ABC，△ACC1的中位，线所以MD∥＝AC，OE∥＝AC，因此MD綊OE．接连OM，而四形从边MDEO平行四形，为边则DE∥MO．因直为线DE⊄平面A1MC，MO⊂平面A1MC，所以直线DE∥平面A1MC．即段线AB上存在一点M(段线AB的中点)，使直线DE∥平面A1MC．[例5]如图，在四棱锥P—ABCD中，△PAD为正三角形，平面PAD⊥平面ABCD，AB∥CD，A...