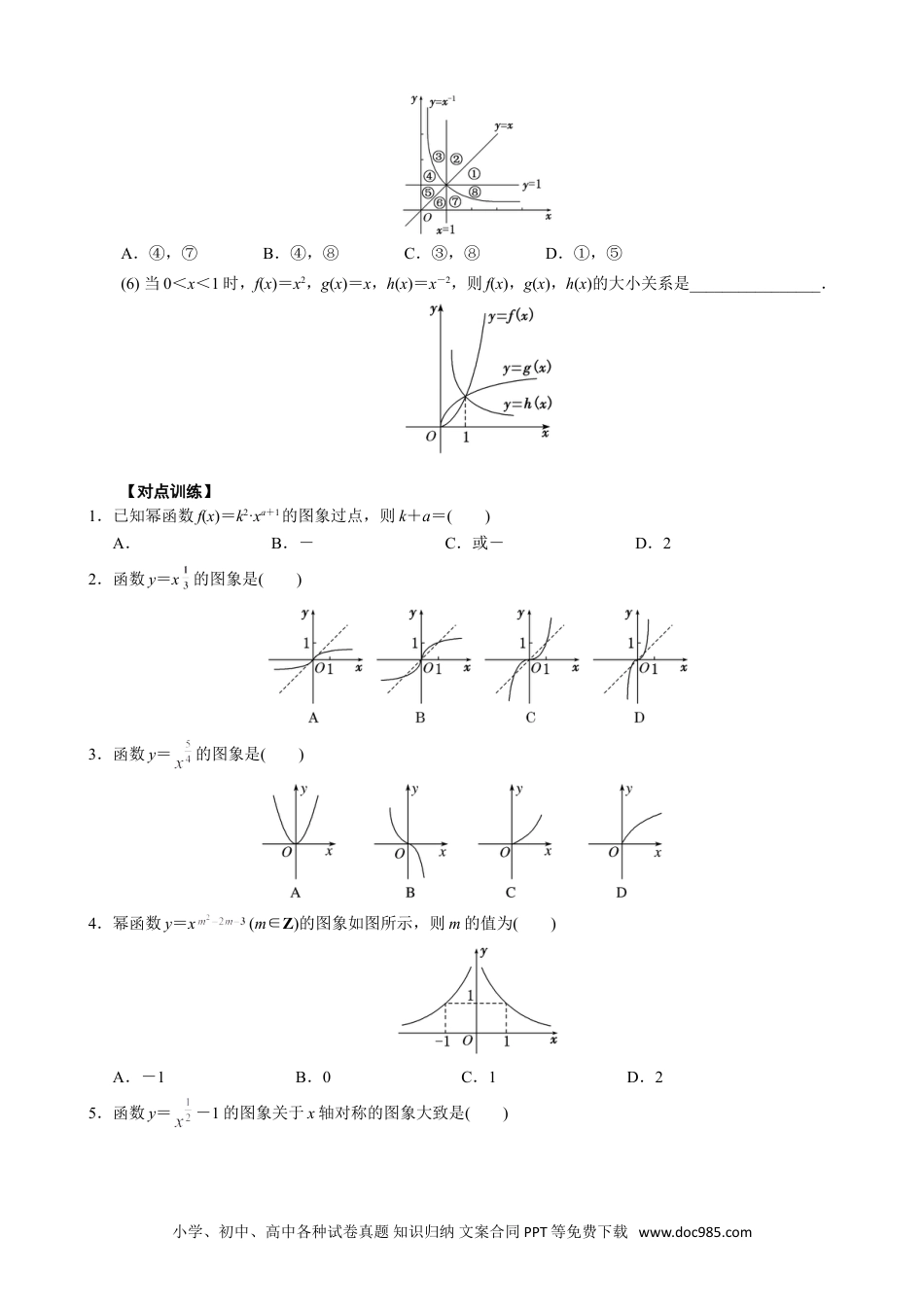
专题十一幂函数1．幂函数的概念一般地，形如y＝xα(α∈R)的函数称为幂函数，其中底数x是自变量，α为常数．2．五种常见幂函数的图象与性质函数特征性质y＝xy＝x2y＝x3y＝xy＝x－1图象定义域RR{x|x≥0}{x|x≠0}值域R{y|y≥0}R{y|y≥0}{y|y≠0}奇偶性奇奇非奇非偶奇单调性增(－∞，0)减，(0，＋∞)增增增(－∞，0)和(0，＋∞)减公共点(1，1)3．常用结论幂函数的图象特征与性质xyy＝1y＝xx＝1α<00<α<1α>1O对于幂函数图象的掌握只要抓住在第一象限内三条线分第一象限为六个区域，即x＝1，y＝1，y＝x分区域．根据α＜0，0＜α＜1，α＝1，α＞1的取值确定位置后，其余象限部分由奇偶性决定．(1)幂函数在(0，＋∞)上都有定义；(2)幂函数的图象过定点(1，1)；(3)当α>0时，幂函数的图象都过点(1，1)和(0，0)，且在(0，＋∞)上单调递增，特别地，当α>1时，幂函数的图象下凸；当0<α<1时，幂函数的图象上凸；(4)当α<0时，幂函数的图象都过点(1，1)，且在(0，＋∞)上单调递减；(5)幂指数互为倒数的幂函数在第一象限内的图象关于直线y＝x对称．(6)在第一象限，作直线x＝a(a>1)，它同各幂函数图象相交，按交点从下到上的顺序，幂指数按从小到大的顺序排列．(7)对于形如f(x)＝xα(其中α∈Z)，当α为奇数时，幂函数为奇函数，图象关于原点对称；当α为偶数时，幂函数为偶函数，图象关于y轴对称．(8)对于形如f(x)＝x(其中m∈N*，n∈Z，m与n互质)的幂函数的奇偶性：①当n为偶数时，f(x)为偶函数，图象关于y轴对称；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com②当m，n都为奇数时，f(x)为奇函数，图象关于原点对称；③当m为偶数时，x>0(或x≥0)，f(x)是非奇非偶函数，图象只在第一象限(或第一象限及原点处)．考点一幂函数的图象及其应用【方法总结】幂函数图象的规律(1)幂函数的图象一定会出现在第一象限，一定不会出现在第四象限，至于是否出现在第二、三象限，要看函数的奇偶性；(2)幂函数的图象最多能同时出现在两个象限内；(3)如果幂函数图象与坐标轴相交，则交点一定是原点；(4)当α为奇数时，幂函数的图象关于原点对称；当α为偶数时，幂函数的图象关于y轴对称．【例题选讲】[例1](1)若幂函数y＝(m2－3m＋3)·xm2－m－2的图象不过原点，则m的取值是()A．－1≤m≤2B．m＝1或m＝2C．m＝2D．m＝1(2)幂函数y＝f(x)的图象过点(4，2)，则幂函数y＝f(x)的图象是()(3)若幂函数y＝x－1，y＝xm与y＝xn在第一象限内的图象如图所示，则m与n的取值情况为()A．－1<m<0<n<1B．－1<n<0<mC．－1<m<0<nD．－1<n<0<m<1(4)如图所示，图中的曲线是幂函数y＝xn在第一象限的图象，已知n取±2，±四个值，则相应于C1，C2，C3，C4的n依次为()A．－2，－，，2B．2，，－，－2C．－，－2，2，D．2，，－2，－(5)幂函数y＝x－1及直线y＝x，y＝1，x＝1将平面直角坐标系的第一象限分成八个“卦限”：①，②，③，④，⑤，⑥，⑦，⑧(如图所示)，则幂函数y＝x的图象经过的“卦限”是()小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．④，⑦B．④，⑧C．③，⑧D．①，⑤(6)当0＜x＜1时，f(x)＝x2，g(x)＝x，h(x)＝x－2，则f(x)，g(x)，h(x)的大小关系是________________．【对点训练】1．已知幂函数f(x)＝k2·xa＋1的图象过点，则k＋a＝()A．B．－C．或－D．22．函数y＝x的图象是()3．函数y＝的图象是()4．幂函数y＝x(m∈Z)的图象如图所示，则m的值为()A．－1B．0C．1D．25．函数y＝－1的图象关于x轴对称的图象大致是()小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com6．图中C1，C2，C3为三个幂函数y＝xk在第一象限内的图象，则解析式中指数k的值依次可以是()A．－1，，3B．－1，3，C．，－1，3D．，3，－17．若四个幂函数y＝xa，y＝xb，y＝xc，y＝xd在同一坐标系中的图象如图所示，则a，b，c，d的大小关系是()A．d>c>b>aB．a>b>c>dC．d>c>a>bD．a>b>d>c8．在同一坐标系内，函数y＝xa(a≠0)和y＝ax－的图象可能是()考点二幂函数性质的综合应用考向1比较幂值大小【方法总结】比较幂值大小的常见类型及解决方法(1)同底不同指：利用...