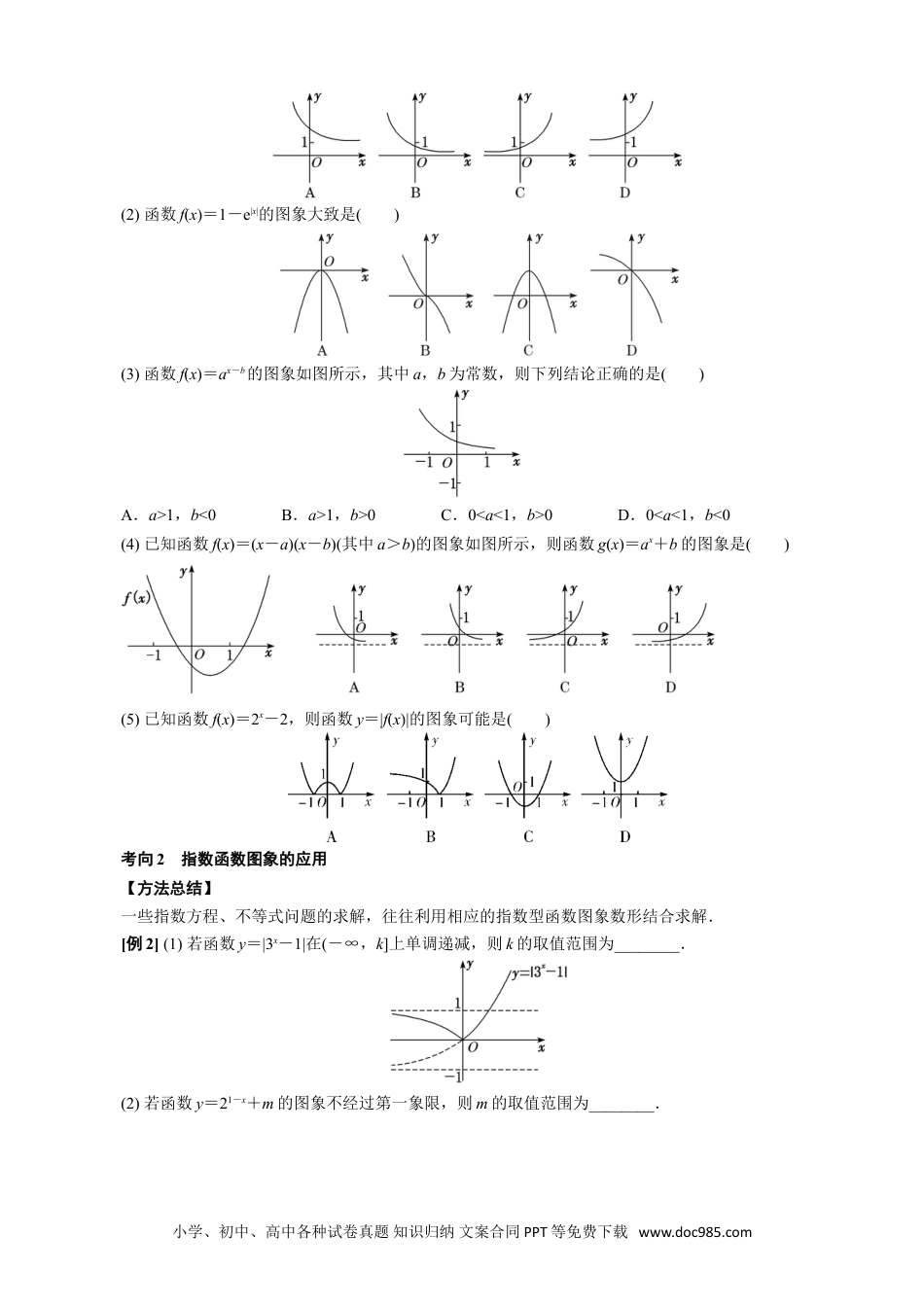
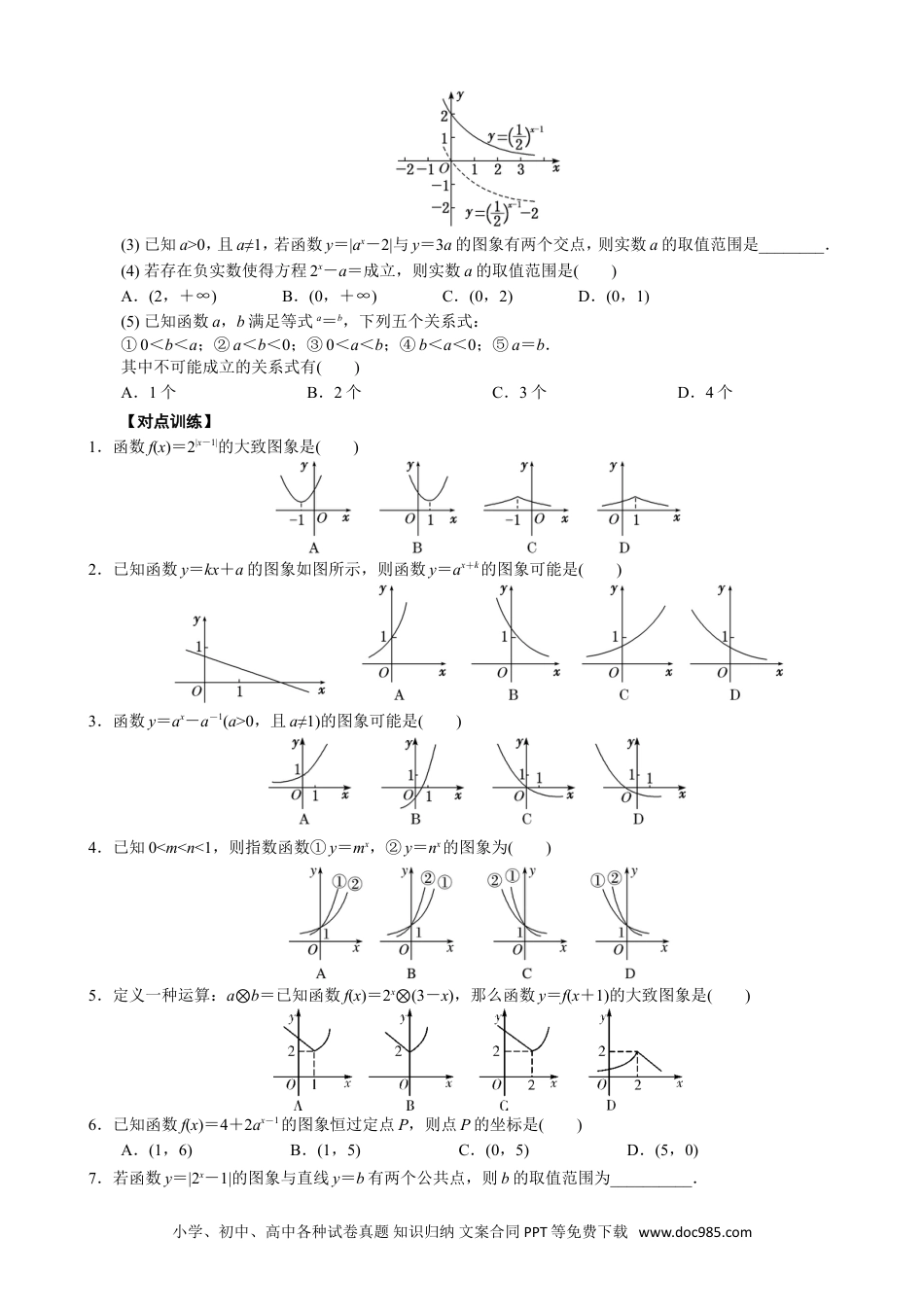
专题十三指数函数考点一指数函数的图象及应用【基本知识】1．指数函数的定义函数y＝ax(a>0，且a≠1)叫做指数函数，其中指数x是自变量，函数的定义域是R，a是底数．2．指数函数的图象函数y＝ax(a>0，且a≠1)0<a<1a>1图象图象特征在x轴上方，过定点(0，1)当x逐渐增大时，图象逐渐下降当x逐渐增大时，图象逐渐上升【常用结论】1．指数函数图象的画法画指数函数y＝ax(a＞0，且a≠1)的图象，应抓住三个关键点：(1，a)，(0，1)，和一条渐近线y＝0．2．底数a与1的大小关系决定了指数函数图象的“升降”：当a>1时，指数函数的图象“上升”；当0<a<1时，指数函数的图象“下降”．3．函数y＝ax与y＝x(a>0，且a≠1)的图象关于y轴对称．4．指数函数的图象与底数大小的比较如图是指数函数(1)y＝ax，(2)y＝bx，(3)y＝cx，(4)y＝dx的图象，底数a，b，c，d与1之间的大小关系为c＞d＞1＞a＞b＞0．由此我们可得到以下规律：在第一象限内，指数函数y＝ax(a＞0，a≠1)的图象越高，底数越大．简称“底大图高”．考向1指数函数图象辨析【方法总结】有关指数函数图象辨析及图象应用的解题思路(1)已知函数解析式判断其图象，一般是取特殊点，判断选项中的图象是否过这些点，若不满足则排除．(2)对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换而得到．特别地，当底数a与1的大小关系不确定时应注意分类讨论．(3)根据指数函数图象判断底数大小的问题，可以通过底大图高进行判断．【例题选讲】[例1](1)函数f(x)＝21－x的大致图象为()小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(2)函数f(x)＝1－e|x|的图象大致是()(3)函数f(x)＝ax－b的图象如图所示，其中a，b为常数，则下列结论正确的是()A．a>1，b<0B．a>1，b>0C．0<a<1，b>0D．0<a<1，b<0(4)已知函数f(x)＝(x－a)(x－b)(其中a＞b)的图象如图所示，则函数g(x)＝ax＋b的图象是()(5)已知函数f(x)＝2x－2，则函数y＝|f(x)|的图象可能是()考向2指数函数图象的应用【方法总结】一些指数方程、不等式问题的求解，往往利用相应的指数型函数图象数形结合求解．[例2](1)若函数y＝|3x－1|在(－∞，k]上单调递减，则k的取值范围为________．(2)若函数y＝21－x＋m的图象不经过第一象限，则m的取值范围为________．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(3)已知a>0，且a≠1，若函数y＝|ax－2|与y＝3a的图象有两个交点，则实数a的取值范围是________．(4)若存在负实数使得方程2x－a＝成立，则实数a的取值范围是()A．(2，＋∞)B．(0，＋∞)C．(0，2)D．(0，1)(5)已知函数a，b满足等式a＝b，下列五个关系式：①0＜b＜a；②a＜b＜0；③0＜a＜b；④b＜a＜0；⑤a＝b．其中不可能成立的关系式有()A．1个B．2个C．3个D．4个【对点训练】1．函数f(x)＝2|x－1|的大致图象是()2．已知函数y＝kx＋a的图象如图所示，则函数y＝ax＋k的图象可能是()3．函数y＝ax－a－1(a>0，且a≠1)的图象可能是()4．已知0<m<n<1，则指数函数①y＝mx，②y＝nx的图象为()5．定义一种运算：a⊗b＝已知函数f(x)＝2x⊗(3－x)，那么函数y＝f(x＋1)的大致图象是()6．已知函数f(x)＝4＋2ax－1的图象恒过定点P，则点P的坐标是()A．(1，6)B．(1，5)C．(0，5)D．(5，0)7．若函数y＝|2x－1|的图象与直线y＝b有两个公共点，则b的取值范围为__________．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com8．已知f(x)＝|2x－1|，当a<b<c时，有f(a)>f(c)>f(b)，则必有()A．a<0，b<0，c<0B．a<0，b>0，c>0C．2－a<2cD．1<2a＋2c<29．若曲线|y|＝2x＋1与直线y＝b没有公共点，则b的取值范围是________．10．如图，在面积为8的平行四边形OABC中，AC⊥CO，AC与BO交于点E．若指数函数y＝ax(a>0，且a≠1)经过点E，B，则a的值为()A．B．C．2D．3考点二指数函数的性质及应用【知识梳理】指数函数的性质函数y＝ax(a>0，且a≠1)0<a<1a>1性质定义域R值域(0，＋∞)单调性在R上是减函数在R上是增函数函数值变化规律当x＝0时，y＝1当x<0时，y>1；当x>0时，0<y<1当x<0时，0<y<1；当x>0时，y>1考...