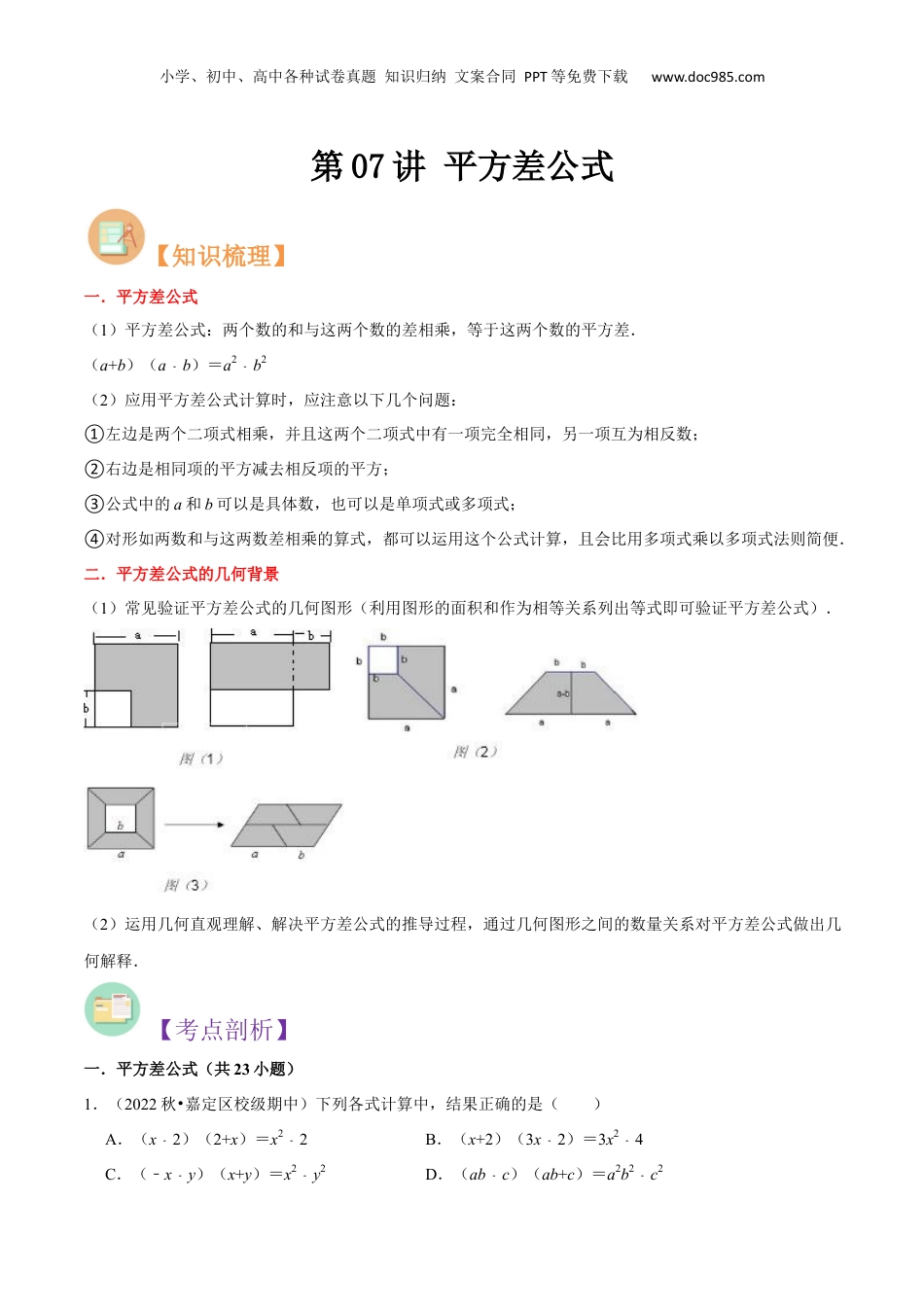
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第07讲平方差公式【知识梳理】一．平方差公式（1）平方差公式：两个数的和与这两个数的差相乘，等于这两个数的平方差．（a+b）（a﹣b）＝a2﹣b2（2）应用平方差公式计算时，应注意以下几个问题：①左边是两个二项式相乘，并且这两个二项式中有一项完全相同，另一项互为相反数；②右边是相同项的平方减去相反项的平方；③公式中的a和b可以是具体数，也可以是单项式或多项式；④对形如两数和与这两数差相乘的算式，都可以运用这个公式计算，且会比用多项式乘以多项式法则简便．二．平方差公式的几何背景（1）常见验证平方差公式的几何图形（利用图形的面积和作为相等关系列出等式即可验证平方差公式）．（2）运用几何直观理解、解决平方差公式的推导过程，通过几何图形之间的数量关系对平方差公式做出几何解释．【考点剖析】一．平方差公式（共23小题）1．（2022秋•嘉定区校级期中）下列各式计算中，结果正确的是（）A．（x2﹣）（2+x）＝x22﹣B．（x+2）（3x2﹣）＝3x24﹣C．（﹣x﹣y）（x+y）＝x2﹣y2D．（ab﹣c）（ab+c）＝a2b2﹣c2小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】根据平方差公式的特征：（1）两个两项式相乘；（2）有一项相同，另一项互为相反数，可利用平方差公式计算即可．【解答】解：A、应为（x2﹣）（2+x）＝x24﹣，故本选项错误；B、（x+2）（3x2﹣）＝3x2+4x4﹣，故本选项错误；C、（﹣x﹣y）（x+y）＝﹣（x+y）2＝﹣x22﹣xy﹣y2，故本选项错误；D、本选项符合平方差公式的特征，并且计算正确，故本选项正确故选：D．【点评】本题考查了平方差公式，运用平方差公式计算时，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方．2．（2021秋•徐汇区校级月考）已知（x﹣ay）（x+ay）＝x216﹣y2，那么a＝±4．【分析】根据平方差公式把左边展开进行解答．【解答】解： x216﹣y2＝（x+4y）（x4﹣y），∴a＝±4，故答案为：±4．【点评】本题考查了平方差公式，关键是利用公式展开求出a的值．3．（2022秋•闵行区期中）计算：（22+1）×（24+1）×（28+1）×（216+1）×（232+1）（结果用幂的形式表示）．【分析】根据平方差公式解答即可．【解答】解：原式＝×（232+1）＝＝＝＝＝．【点评】此题考查平方差公式，关键是根据平方差公式解答．4．（2022秋•浦东新区期中）若a＝（﹣1）2022，b＝2021×20232022﹣2，c＝82022×（﹣0.125）2023，则a、小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comb、c的大小关系是a＞c＞b（用“＞”连接）．【分析】根据指数幂的意义、平方差公式、积的乘方的运算法则，求出a、b、c的值，再根据求出的结果和实数的大小比较法则比较大小即可．【解答】解：a＝（﹣1）2022＝1，b＝2021×20232022﹣2＝（20221﹣）（2022+1）﹣20222＝2022212022﹣﹣2＝﹣1，c＝82022×（﹣0.125）2023＝﹣0.125×（﹣0.125×8）2022＝﹣0.125，1 ﹣＜﹣0.125＜1，∴a＞c＞b，故答案为：a＞c＞b．【点评】本题考查了指数幂、平方差公式、积的乘方和实数的大小比较，能求出a、b、c的值和能熟记实数的大小比较法则是解此题的关键，注意：正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．5．（2022秋•宝山区校级期中）计算：＝﹣a2．【分析】先提取公因式﹣1，再利用平方差公式计算即可．【解答】解：原式＝﹣（a﹣）（a+）＝﹣（a2﹣）＝﹣a2．故答案为：﹣a2．【点评】此题考查的是平方差公式，两个数的和与这两个数的差相乘，等于这两个数的平方差．6．（2021秋•普陀区校级月考）计算：（2m﹣n）（2m+n）＝4m2﹣n2．【分析】根据平方差公式进行计算．【解答】解：原式＝（2m）2﹣n2＝4m2﹣n2，故答案为：4m2﹣n2．【点评】本题考查平方差公式，掌握平方差公式（a+b）（a﹣b）＝a2﹣b2的结构是解题关键．7．（2022秋•上海期末）计算：（x2﹣y）（x+2y）﹣x（x﹣y）．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析...