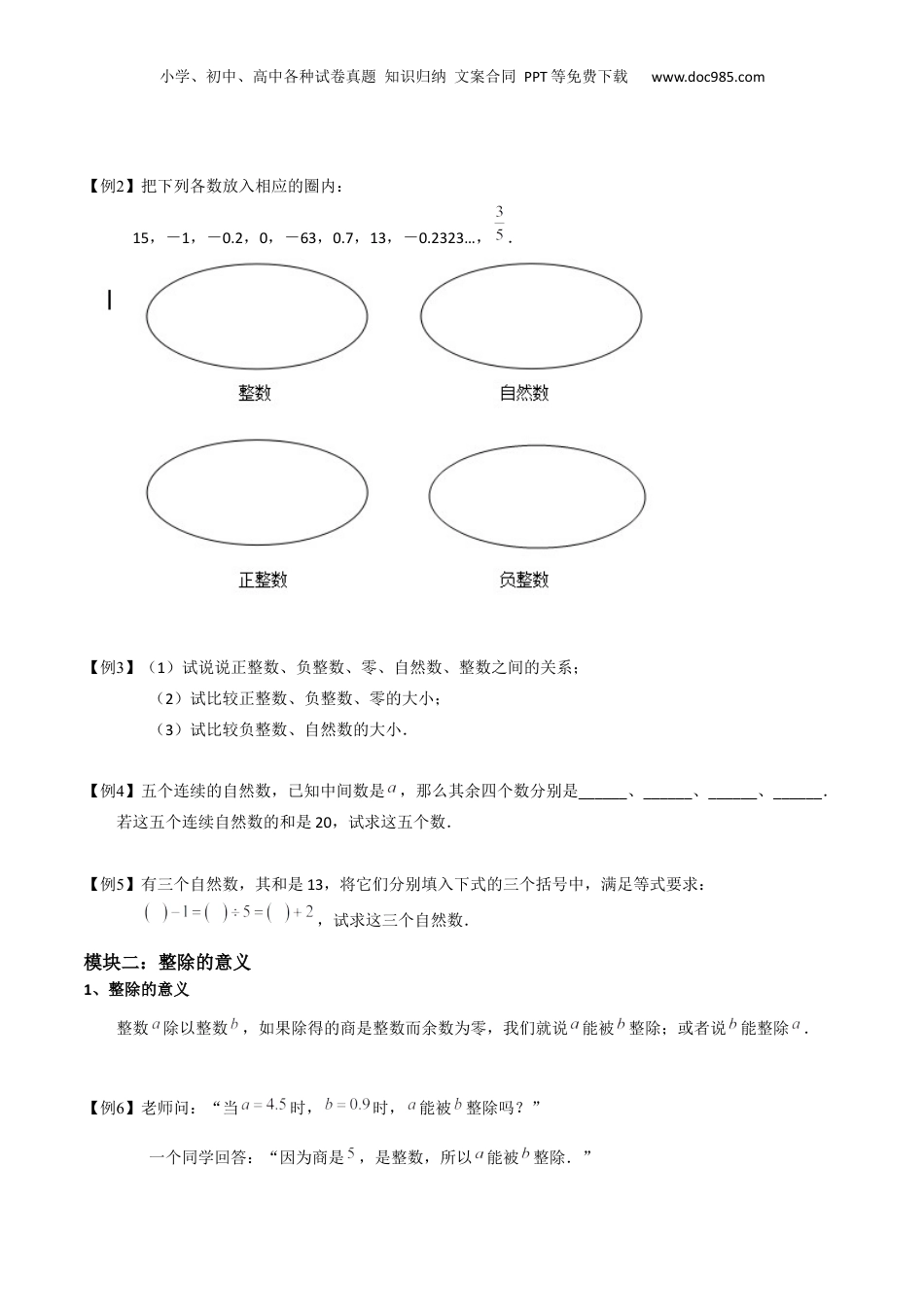
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com《小升初数学无忧衔接（沪教版）》专题01整数和整除【内容分析】整数和整除是六年级数学上学期第一章第一节内容，主要对整数的分类和整除的概念进行讲解，重点是整除的概念理解，难点是整除条件的归纳总结．通过这节课的学习一方面为我们后期学习公因数和公倍数提供依据，另一方面也为后面学习有理数奠定基础．【知识结构】模块一：整数的意义和分类1、整数的意义和分类（1）自然数：零和正整数统称为自然数；（2）整数：正整数、零、负整数，统称为整数．【例1】判断题（若是正确的，请说明理由；若是错误的，请把它改正确）．（1）最小的自然数是1；（2）最小的整数是0；（3）非负整数是自然数；（4）有最大的正整数，但没有最小的负整数；（5）有最小的正整数，但没有最大的负整数．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例2】把下列各数放入相应的圈内：15，－1，－0.2，0，－63，0.7，13，－0.2323…，．【例3】（1）试说说正整数、负整数、零、自然数、整数之间的关系；（2）试比较正整数、负整数、零的大小；（3）试比较负整数、自然数的大小．【例4】五个连续的自然数，已知中间数是，那么其余四个数分别是______、______、______、______．若这五个连续自然数的和是20，试求这五个数．【例5】有三个自然数，其和是13，将它们分别填入下式的三个括号中，满足等式要求：，试求这三个自然数．模块二：整除的意义1、整除的意义整数除以整数，如果除得的商是整数而余数为零，我们就说能被整除；或者说能整除．【例6】老师问：“当时，时，能被整除吗？”一个同学回答：“因为商是，是整数，所以能被整除．”小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com你认为对吗？【例7】下列各组数中，如果第一个数能被第二个数整除，请在下面的（）内打“√”，不能整除的打“×”．18和9（）15和30（）0．4和4（）14和6（）17和35（）9和0．5（）【例8】已知下列除法算式：57÷7=8……1；21÷7=3；22÷0.2=110；22÷5=4.4；0÷3=0；2÷4=0.5．（1）表示能除尽的算式有哪几个？（2）哪些算式中可以说被除数能被除数整除？【例9】把表示下列算式的序号填入适当的空格内．（1）30÷10；（2）7÷25；（3）35÷0．1；（4）18÷3；（5）0．4÷2；（6）3．9÷0．3；（7）27÷9；（8）16÷4．除数能整除被除数的：________________________________________；能够除尽的：________________________________________________．1、整除的条件是什么？2、“a能整除b”与“a能被b整除”的区别是什么？师生总结小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例10】若两个整数a、b()都能被整数c整除，它们的和、差、积也能被c整除吗？为什么？【例11】一个两位数，能被5整除，其个位数字减十位数字的差是正整数中最小的偶数，求这个两位数．【例12】15支铅笔分给几个学生，每人发的一样多且不止1支，并且正好分完，可以分给几个人？每人几支？有几种分法？【例13】2015年的教师节是星期四，老师们可以好好庆祝一下自己的节日了，同学们，明年呢？我们能否不查日历，就能知道2016年的教师节是星期几呢？1、整除与除尽有什么相同点？2、除与除尽有什么不同点？师生总结小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例14】学校有10个兴趣小组，各组的人数如下表：一天下午，学校同时举办语文写作和英语听力两个讲座，已知有9个小组去听讲座，其中听英语讲座的人数是听语文讲座人数的6倍，还剩下一个小组在教室里讨论问题，这一组是第几组？模块三：因数和倍数的意义1、因数和倍数的意义整数能被整数整除，就叫做的倍数，就叫做的因数（也称为约数）．【例15】有一个算式，则可以说______能被______整除，也可以说______能整除______，还可以说______和______是______的因数，______是______和______的倍数．【例16】分别写出12、19和36的因数，再分别写出这三个数的倍数（倍数只需从小到大依次写3...