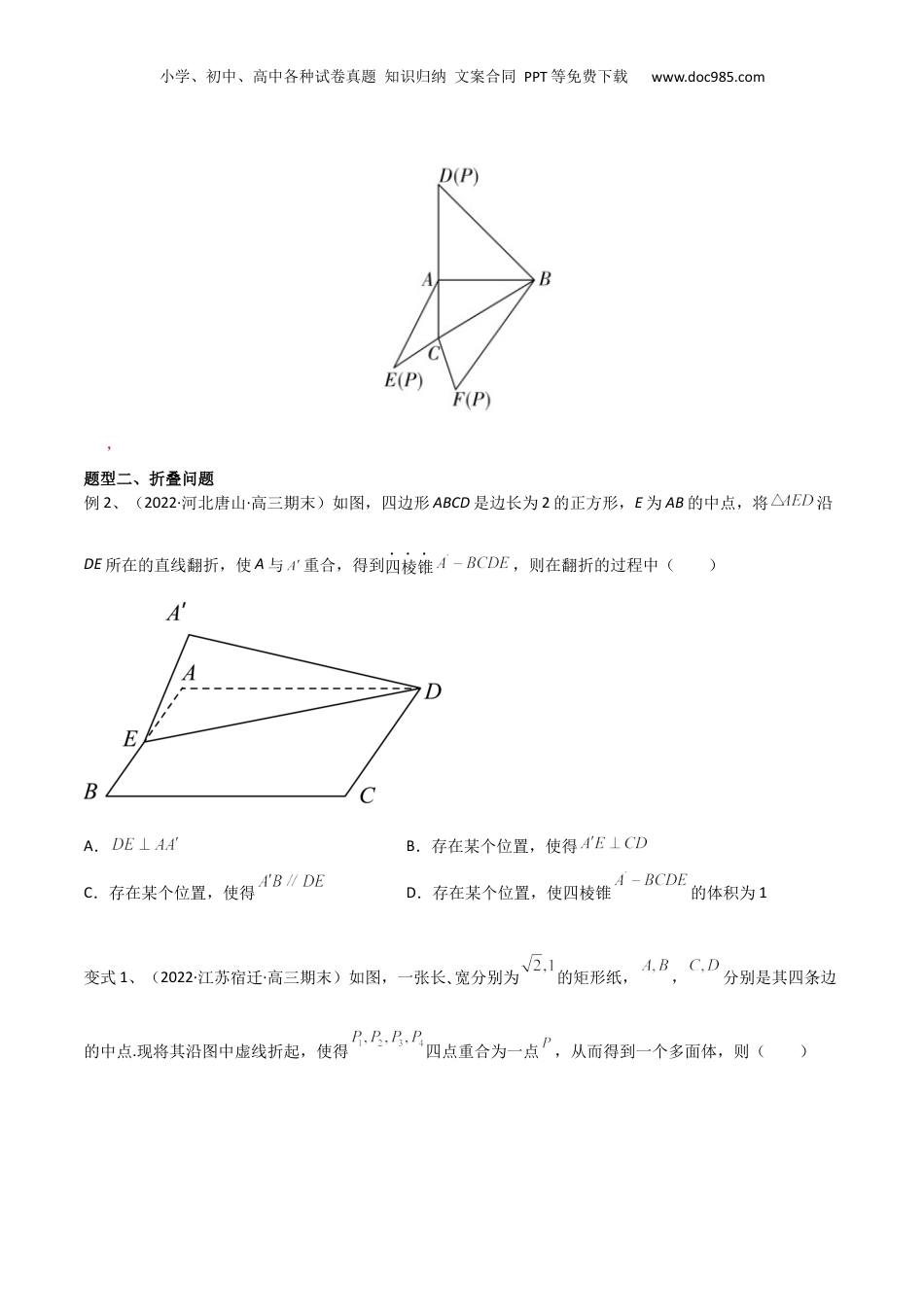
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第57讲立体几何中翻折问题（微专题）一、题型选讲题型一、展开问题例1、（2022·广东佛山·高三期末）长方体中，，E为棱上的动点，平面交棱于F，则四边形的周长的最小值为（）A．B．C．D．变式1、（2022·湖北武昌·高三期末）已知四面体ABCD的一个平面展开图如图所示，其中四边形AEFD是边长为的菱形，B，C分别为AE，FD的中点，，则在该四面体中（）A．B．BE与平面DCE所成角的余弦值为C．四面体ABCD的内切球半径为D．四面体ABCD的外接球表面积为变式2、【2020年高考全国Ⅰ卷理数】如图，在三棱锥P–ABC的平面展开图中，AC=1，，AB⊥AC，AB⊥AD，∠CAE=30°，则cos∠FCB=______________.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，题型二、折叠问题例2、（2022·河北唐山·高三期末）如图，四边形ABCD是边长为2的正方形，E为AB的中点，将沿DE所在的直线翻折，使A与重合，得到四棱锥，则在翻折的过程中（）A．B．存在某个位置，使得C．存在某个位置，使得D．存在某个位置，使四棱锥的体积为1变式1、（2022·江苏宿迁·高三期末）如图，一张长､宽分别为的矩形纸，，分别是其四条边的中点.现将其沿图中虚线折起，使得四点重合为一点，从而得到一个多面体，则（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．在该多面体中，B．该多面体是三棱锥C．在该多面体中，平面平面D．该多面体的体积为变式2、（2022·江苏海安·高三期末）如图，ABCD是一块直角梯形加热片，AB∥CD，∠DAB＝60°，AB＝AD＝4dm．现将△BCD沿BD折起，成为二面角A－BD－C是90°的加热零件，则AC间的距离是________dm；为了安全，把该零件放进一个球形防护罩，则球形防护罩的表面积的最小值是________dm2．（所有器件厚度忽略不计）变式3、（2022·河北保定·高三期末）如图，是边长为4的等边三角形的中位线，将沿折起，使得点与重合，平面平面，则四棱雉外接球的表面积是___________.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题型三、折叠的综合性问题例3、（2022·江苏扬州·高三期末）在边长为6的正三角形ABC中M，N分别为边AB，AC上的点，且满足，把△AMN沿着MN翻折至A′MN位置，则下列说法中正确的有（）A．在翻折过程中，在边A′N上存在点P，满足CP∥平面A′BMB．若，则在翻折过程中的某个位置，满足平面A′BC⊥平面BCNMC．若且二面角A′－MN－B的大小为120°，则四棱锥A′－BCNM的外接球的表面积为61πD．在翻折过程中，四棱锥A′－BCNM体积的最大值为变式1、（2021·山东滨州市·高三二模）已知正方形ABCD的边长为2，将ACD△沿AC翻折到ACD△的位置，得到四面体DABC，在翻折过程中，点D�始终位于ABC所在平面的同一侧，且BD的最小值为2，则下列结论正确的是（）A．四面体DABC的外接球的表面积为8B．四面体DABC体积的最大值为63C．点D的运动轨迹的长度为22π3D．边AD旋转所形成的曲面的面积为22π3变式2、【2022·广东省深圳市宝安区第一次调研10月】如图甲是由正方形，等边和等边组成的一个平面图形，其中，将其沿，，折起得三棱锥，如图乙.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）求证：平面平面；（2）过棱作平面交棱于点，且三棱锥和的体积比为，求直线与平面所成角的正弦值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com