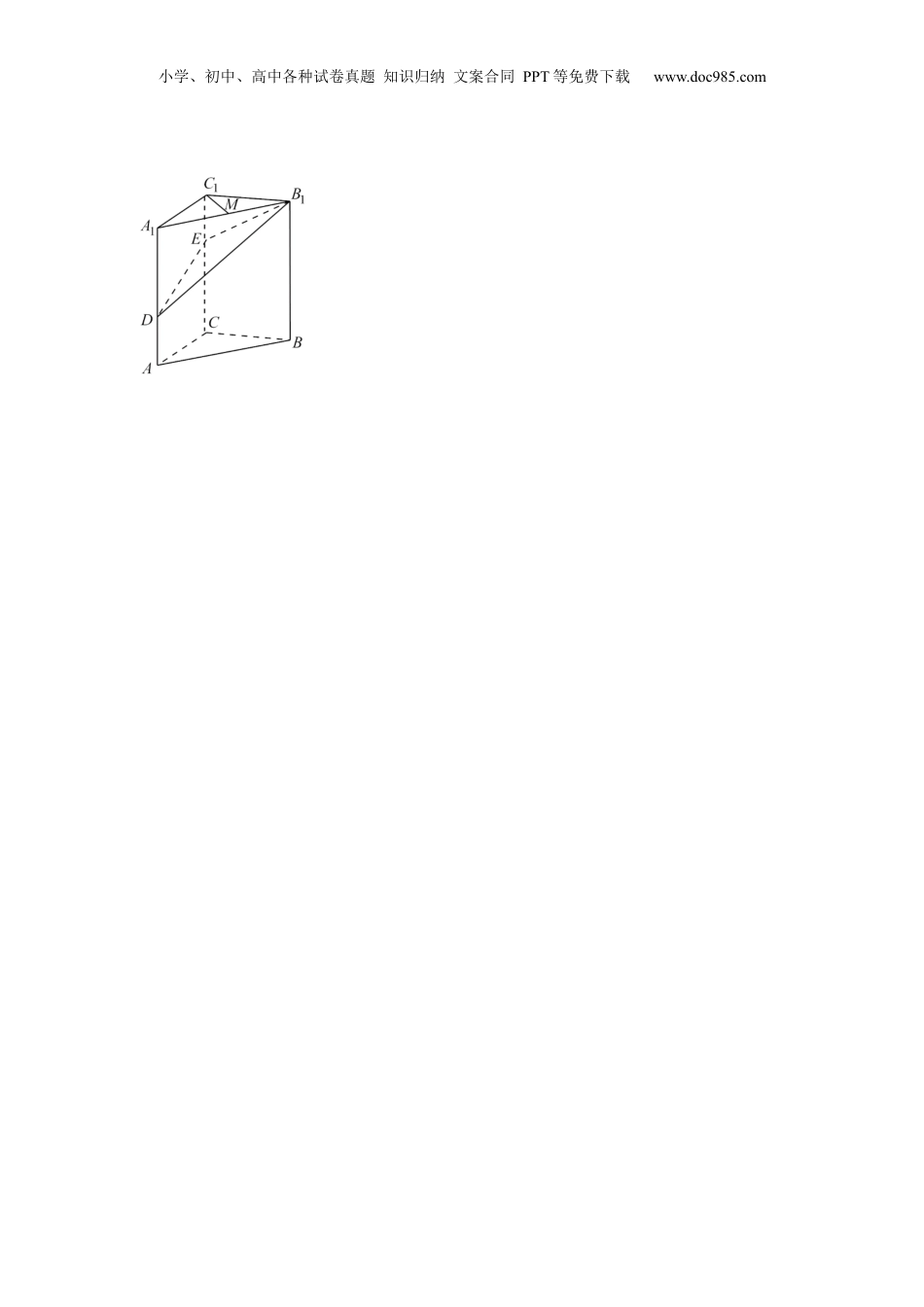
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com重难点突破04立体几何表面积与体积1．《九章算术》中记载，四个面都为直角三角形的四面体称之为鳖臑．现有一个“鳖臑”，底面，，且，，则该四面体的体积为A．1B．2C．4D．82．已知圆柱的底面半径为2，母线长为8，过圆柱底面圆周上一点作与圆柱底面所成角为的平面，把这个圆柱分成两个几何体，则两几何体的体积之比为A．B．C．D．3．四棱锥的底面是平行四边形，点、分别为、的中点，连接交的延长线于点，平面将四棱锥分成两部分的体积分别为，且满足，则A．B．C．D．二．多选题（共1小题）4．如图，在棱长为1的正方体中，点满足，其中，，，，则小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．当时，B．当，时，点到平面的距离为C．当时，平面D．当时，三棱锥的体积恒为三．填空题（共1小题）5．四棱锥的底面是平行四边形，点、分别为、的中点，平面将四棱锥分成两部分的体积分别为，且满足，则．四．解答题（共15小题）6．如图，在三棱柱中，平面，，，，点，分别在棱和棱上，且，，为棱的中点．（1）求证：；（2）求三棱锥的体积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com7．如图，在四棱锥中，，，，平面平面．（1）求证：平面；（2）设，，求三棱锥的体积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com8．如图，在正四棱锥中，，分别为，的中点，．（1）证明：，，，四点共面．（2）记四棱锥的体积为，四棱锥的体积为，求的值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com9．《九章算术》作为中国古代数学专著之一，在其“商功”篇内记载：“斜解立方，得两堑堵．斜解堑堵，其一为阳马，一为鳖臑．”鳖臑是我国古代数学对四个面均为直角三角形的四面体的统称．如图所示，是长方体．（1）求证：三棱锥为鳖臑；（2）若，，，求三棱锥的表面积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com10．如图1，在中，，分别为，的中点；为的中点，，，将沿折起到△的位置，使得平面平面，如图2，点是线段上的一点（不包含端点）．（1）求证：；（2）若直线和平面所成角的正弦值为，求三棱锥的体积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com11．如图，在棱长为1的正方体中，点平面，且满足．（1）利用向量基本定理求的值；（2）求三棱锥的体积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com12．如图，三棱锥的底面和侧面都是边长为2的等边三角形，，分别是，的中点，．（1）证明：平面；（2）求三棱锥的体积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com13．如图，在四棱锥中，底面为直角梯形，，，侧面面，，，为的中点．（1）求证：面面；（2）若二面角的大小为，求与面所成角的正弦值；（3）若平面与平面所成的锐二面角大小为，求四棱锥的体积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com14．劳动教育是中国特色社会主义教育制度的重要内容，对于培养社会主义建设者和接班人具有重要战略意义，为了使学生熟练掌握一定劳动技能，理解劳动创造价值，某普通高中组织学生到工厂进行实践劳动．在设计劳动中，某学生欲将一个底面半径为，高为的实心圆锥体工件切割成一个圆柱体，并使圆柱体的一个底面落在圆锥体的底面内．（1）求该圆柱的侧面积的最大值；（2）求该圆柱的体积的最大值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com15．如图，在多面体中，四边形与均为直角梯形，，，平面，，．（1）已知点为上一点，且，求证：与平面不平行；（2）已知直线与平面所成角的正弦值为，求该多面体的体积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com16．已知四棱锥，底面是菱形，，底面，...