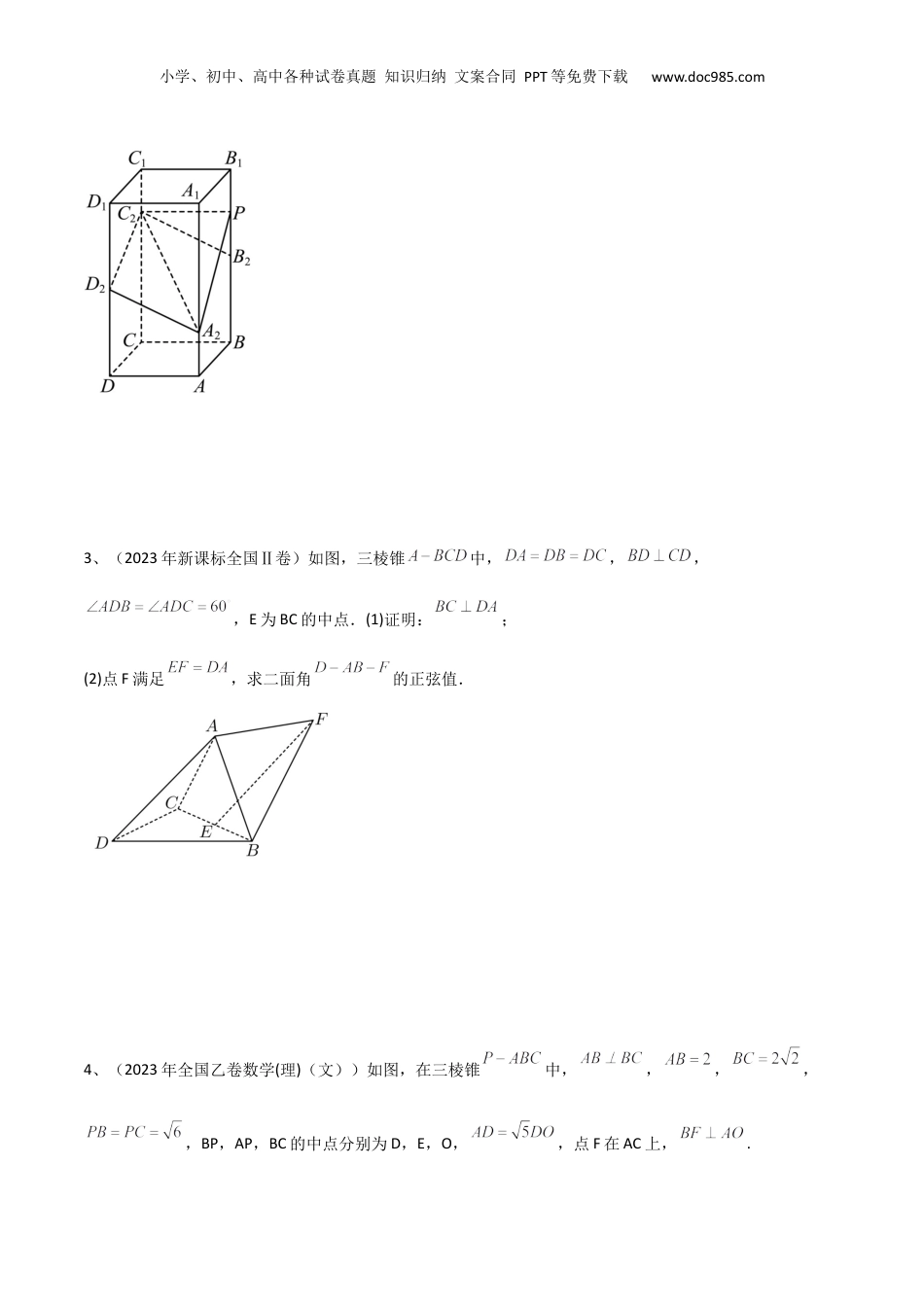
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题12运用空间向量研究立体几何问题（1）1、（2023年全国甲卷数学（理））在三棱柱中，，底面ABC，，到平面的距离为1．(1)求证：；(2)若直线与距离为2，求与平面所成角的正弦值．2、（2023年新课标全国Ⅰ卷）如图，在正四棱柱中，．点分别在棱,上，．(1)证明：；(2)点在棱上，当二面角为时，求．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3、（2023年新课标全国Ⅱ卷）如图，三棱锥中，，，，E为BC的中点．(1)证明：；(2)点F满足，求二面角的正弦值．4、（2023年全国乙卷数学(理)（文））如图，在三棱锥中，，，，，BP，AP，BC的中点分别为D，E，O，，点F在AC上，.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明：平面；(2)证明：平面平面BEF；(3)求二面角的正弦值.5、【2022年全国甲卷】在四棱锥P−ABCD中，PD⊥底面ABCD,CD∥AB,AD=DC=CB=1,AB=2,DP=❑√3．(1)证明：BD⊥PA；(2)求PD与平面PAB所成的角的正弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com6、【2022年全国乙卷】如图，四面体ABCD中，AD⊥CD,AD=CD,∠ADB=∠BDC，E为AC的中点．(1)证明：平面BED⊥平面ACD；(2)设AB=BD=2,∠ACB=60°，点F在BD上，当△AFC的面积最小时，求CF与平面ABD所成的角的正弦值．7、【2022年新高考1卷】如图，直三棱柱ABC−A1B1C1的体积为4，△A1BC的面积为2❑√2．(1)求A到平面A1BC的距离；(2)设D为A1C的中点，AA1=AB，平面A1BC⊥平面ABB1A1，求二面角A−BD−C的正弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com8、【2022年新高考2卷】如图，PO是三棱锥P−ABC的高，PA=PB，AB⊥AC，E是PB的中点．(1)证明：OE/¿平面PAC；(2)若∠ABO=∠CBO=30°，PO=3，PA=5，求二面角C−AE−B的正弦值．题组一、线面角1-1、（2023·安徽宿州·统考一模）如图，四棱锥中，底面ABCD，，，，，为棱靠近点的三等分点.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明：平面；(2)求与平面所成的角的正弦值.1-2、（2023·吉林通化·梅河口市第五中学校考一模）如图，在正三棱柱中，D为棱上的点，E，F，G分别为AC，，的中点，．(1)求证：；(2)若直线FG与平面BCD所成角的正弦值为，求AD的长．1-3、（2023·山西晋中·统考三模）如图，在四棱锥P-ABCD中，底面ABCD为矩形，E是CD的中点，AE与BD交于点F，G是的重心．(1)求证：平面PCD；(2)若平面PAD⊥平面ABCD，为等腰直角三角形，且，求直线AG与平面PBD所成角的正弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题组二、面面角2-1、（2023·黑龙江大庆·统考一模）如图，在长方体中，底面是边长为2的正方形，，，分别是，的中点.(1)证明：∥平面；(2)求平面与平面夹角的余弦值.2-2、（2023·山西临汾·统考一模）在三棱锥中，，，，取直小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com线与的方向向量分别为，，若与夹角为.(1)求证：；(2)求平面与平面的夹角的余弦值.2-3、（2023·云南红河·统考一模）如图，在多面体ABCDEF中，A，B，C，D四点共面，，，AF⊥平面ABCD，．(1)求证：CD⊥平面ADF；(2)若，，求平面和平面的夹角的余弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题组三、线面角与面面角的综合3-1、（2023·湖南邵阳·统考三模）如图所示，在直四棱柱ABCD-中，底面ABCD为菱形，，，E为线段上一点.(1)求证：；3-2、（2023·湖南岳阳·统考三模）如图，在三棱柱中，D为AC的中点，AB=BC=2，.(1)证明：；(2)若，且满足：三棱柱的体积为，二面角的大小为60°，求二面角小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com的正弦值.1、（2022·山东青岛·高三期末）如图所示，已知四棱锥P-ABCD的底面是矩形，底面ABCD，M为BC中点，且.（1）求证：面面PDB；（2）若两条异面直线AB与PC所成的角为45...