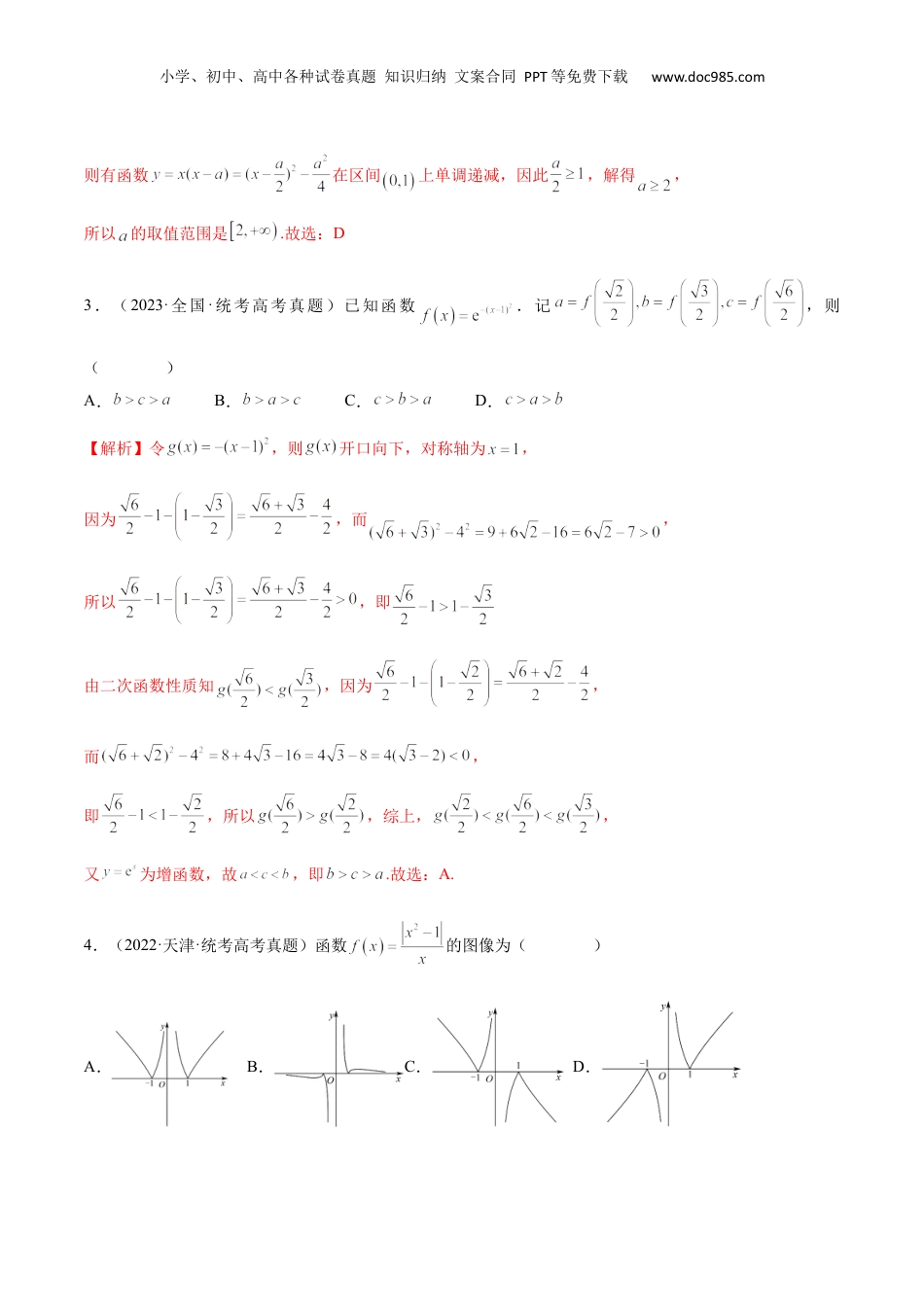
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题06函数的单调性真题再现一、单选题1．（2023·北京·统考高考真题）下列函数中，在区间上单调递增的是（）A．B．C．D．【解析】对于A，因为在上单调递增，在上单调递减，所以在上单调递减，故A错误；对于B，因为在上单调递增，在上单调递减，所以在上单调递减，故B错误；对于C，因为在上单调递减，在上单调递减，所以在上单调递增，故C正确；对于D，因为，，显然在上不单调，D错误.故选：C.2．（2023·全国·统考高考真题）设函数在区间上单调递减，则的取值范围是（）A．B．C．D．【解析】函数在R上单调递增，而函数在区间上单调递减，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则有函数在区间上单调递减，因此，解得，所以的取值范围是.故选：D3．（2023·全国·统考高考真题）已知函数．记，则（）A．B．C．D．【解析】令，则开口向下，对称轴为，因为，而，所以，即由二次函数性质知，因为，而，即，所以，综上，，又为增函数，故，即.故选：A.4．（2022·天津·统考高考真题）函数的图像为（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解析】函数的定义域为，且，函数为奇函数，A选项错误；又当时，，C选项错误；当时，函数单调递增，故B选项错误；故选：D.5．（2021·全国·高考真题）下列函数中是增函数的为（）A．B．C．D．【解析】对于A，为上的减函数，不合题意，舍.对于B，为上的减函数，不合题意，舍.对于C，在为减函数，不合题意，舍.对于D，为上的增函数，符合题意，故选：D.考点一判断或证明函数的单调性一、单选题1．下列函数中，在区间上为增函数的是（）A．B．C．D．【解析】由于在为单调递减函数，在时无意义，A错误；在为单调递增函数，B正确；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com定义域为，在无意义，C错误；在为单调递减函数，D错误，故选：B2．下列函数中，是奇函数且在区间上单调递增的是（）A．B．C．D．【解析】对于A，在区间上不是单调的，故A错；对于B，，定义域不关于原点对称，不是奇函数，故B错；对于C，在区间上单调递减，故C错；对于D，，是奇函数且在区间上单调递增，故D对；故选：D.3．在下列函数中：①，②，③，④，在上为增函数的有（）A．①②B．③④C．②③D．①④【解析】因为，所以①在上单调递减，不符合题意；②在上为常函数，不符合题意；③在上单调递增，符合题意；④在上单调递增，符合题意；故符合题意的为③④.故选：B.二、解答题小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4．已知定义在上的函数是奇函数.(1)求实数，的值；(2)判断在上的单调性并用定义证明；(3)若对任意的，不等式恒成立，求实数的取值范围.【解析】（1）由题意，定义域为的函数是奇函数，得，，∴，，经检验知，是奇函数.故.（2）由（1）知，，函数在上是减函数.证明如下：设，则， ，∴，又，所以，即.∴函数在上是减函数.（3）由，且是奇函数，得， 在上是减函数，所以对任意的恒成立，即对任意的恒成立，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com由，得，∴，所以，故得实数的取值范围.5．已知函数在为奇函数，且(1)求值；(2)判断函数在的单调性，并用定义证明；(3)解关于t的不等式【解析】（1）在为奇函数，，解得：，又，解得：，故，经检验满足题设.（2）当时，，当时函数在为奇函数，由，判断函数在为单调递减，证明：，，，，，，函数在为单调递减，（3）则，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com在为奇函数，，又函数在为单调递减，，t的不等式的解集为6．已知函数的定义域是，满足，时，对任意正实数x，y，都有．(1)求的值；(2)证明：函数在上是增函数；(3)求不等式的解集．【解析】（1）因为对任意正实数x，y，都有，所以，即，因为，所以.（2）由得，任取，且，则，，即，所以函数在上是增函数；（3）由（1）知，，因为，所以，即，由...