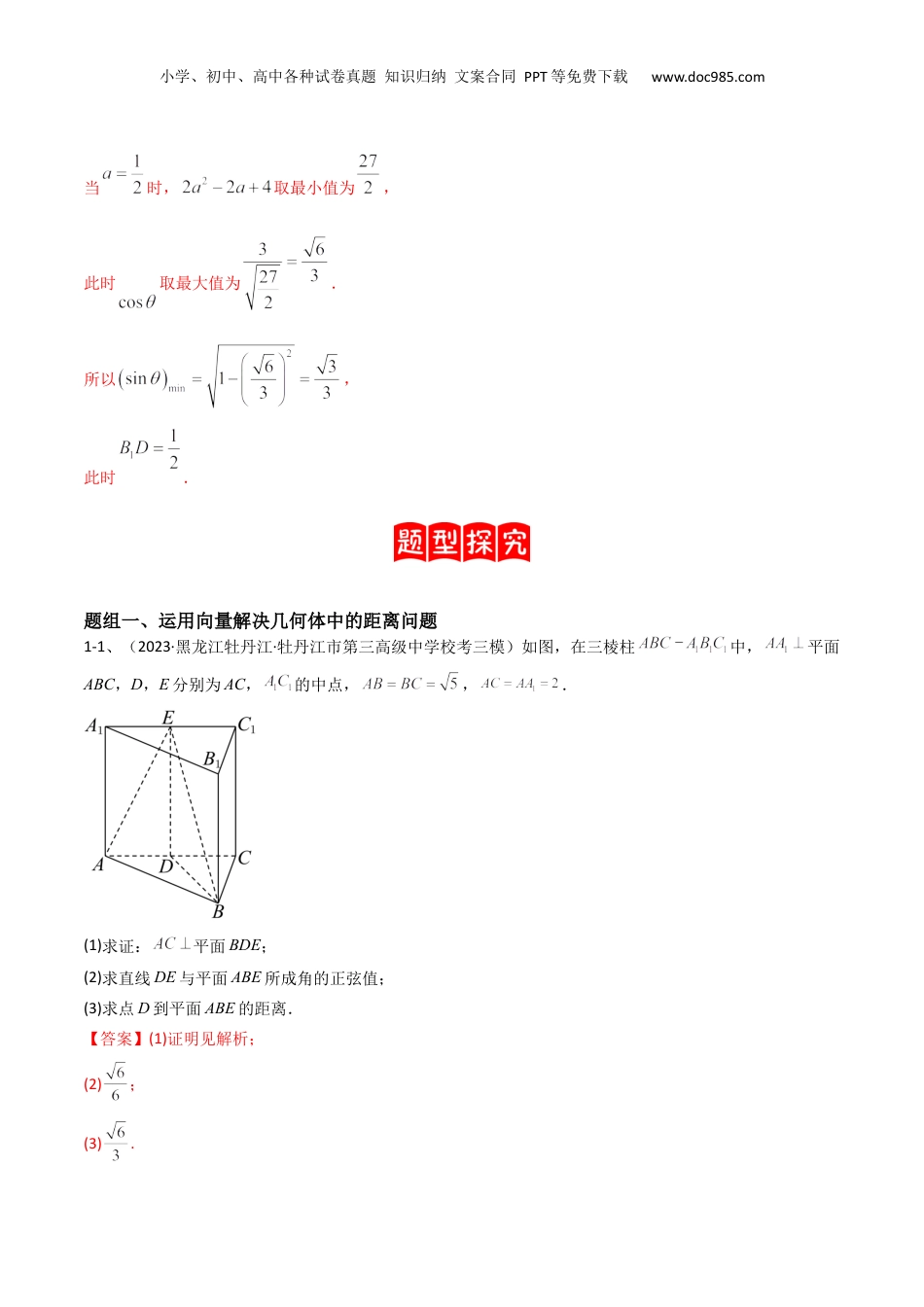
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题13运用空间向量研究立体几何问题（2）1、（2021年全国高考甲卷数学（理）试题）已知直三棱柱中，侧面为正方形，，E，F分别为和的中点，D为棱上的点．（1）证明：；（2）当为何值时，面与面所成的二面角的正弦值最小?【解析】因为三棱柱是直三棱柱，所以底面，所以因为，，所以，又，所以平面．所以两两垂直．以为坐标原点，分别以所在直线为轴建立空间直角坐标系，如图．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以，．由题设（）．（1）因为，所以，所以．（2）设平面的法向量为，因为，所以，即．令，则因为平面的法向量为，设平面与平面的二面角的平面角为，则．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com当时，取最小值为，此时取最大值为．所以，此时．题组一、运用向量解决几何体中的距离问题1-1、（2023·黑龙江牡丹江·牡丹江市第三高级中学校考三模）如图，在三棱柱中，平面ABC，D，E分别为AC，的中点，，．(1)求证：平面BDE；(2)求直线DE与平面ABE所成角的正弦值；(3)求点D到平面ABE的距离．【答案】(1)证明见解析；(2)；(3).小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【详解】（1）在三棱柱中，，为，的中点，∴， 平面，∴平面， 平面，∴，在三角形中，，为中点，∴， ，平面，∴平面.（2）如图，以为原点，分别以为轴建立空间直角坐标系，在直角三角形中，，，∴，，，，，，，，设平面的法向量为，，令，则，，所以，设直线与平面所成角为，所以.（3）设点到平面的距离为，所以.1-2、（2023·安徽黄山·统考三模）如图，在直角梯形中，，，四边形为平行四边形，对角线和相交于点，平面平面，，，是线段上一动点（不含端点）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)当点为线段的中点时，证明：//平面；(2)若，，且直线与平面成角，求二面角的正弦值．【答案】(1)证明见解析(2)【详解】（1）证明：因为四边形为平行四边形，所以是中点，连接，又点为线段的中点，则，且又且，所以，所以四边形是平行四边形，所以，又平面，平面，所以平面.（2）以为原点，为轴建立空间直角坐标系（如图）.则有，设，，则，为平面的法向量，所以，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com解得（其中舍去）.所以设平面的法向量为，则有，，故可取.设平面的法向量为，则有，，故可取所以.所以二面角的正弦值为1-3、（2023·四川成都·四川省成都列五中学校考三模）如图，四棱柱的侧棱⊥底面ABCD，四边形ABCD为菱形，E，F分别为，的中点.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明：四点共面；(2)若，求点A到平面的距离.【答案】(1)证明见解析(2)【详解】（1）取的中点为G，连接AG，GE，由E，G分别为，的中点，所以EGDCAB∥∥，且，所以四边形ABEG为平行四边形，故，又因为F是的中点，所以，所以，故B，F，，E四点共面.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）易知四边形为菱形，且，，，，所以菱形的面积为，设点到平面BEF的距离为，点B到平面距离为，且，由，得：，因为，，所以，又因为，，、面，所以面，所以，所以.故点A到平面的距离为题组二、最值问题2-1、（2022·江苏扬州·高三期末）如图，在三棱台ABC－A1B1C1中，底面△ABC是等腰三角形，且BC＝8，AB＝AC＝5，O为BC的中点．侧面BCC1B1为等腰梯形，且B1C1＝CC1＝4，M为B1C1中点．（1）证明：平面ABC⊥平面AOM；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）记二面角A－BC－B1的大小为θ，当θ∈[，]时，求直线BB1平面AA1C1C所成角的正弦的最大值．【答案】（1）证明见解析；（2）.【分析】（1）利用线面垂直的判定定理及面面垂直的判定定理即证；（2）设直线BB1与平面AA1C1C所成的角为α，利用坐标法可求，然后利用导函数求最值即得.（1） △ABC是等...