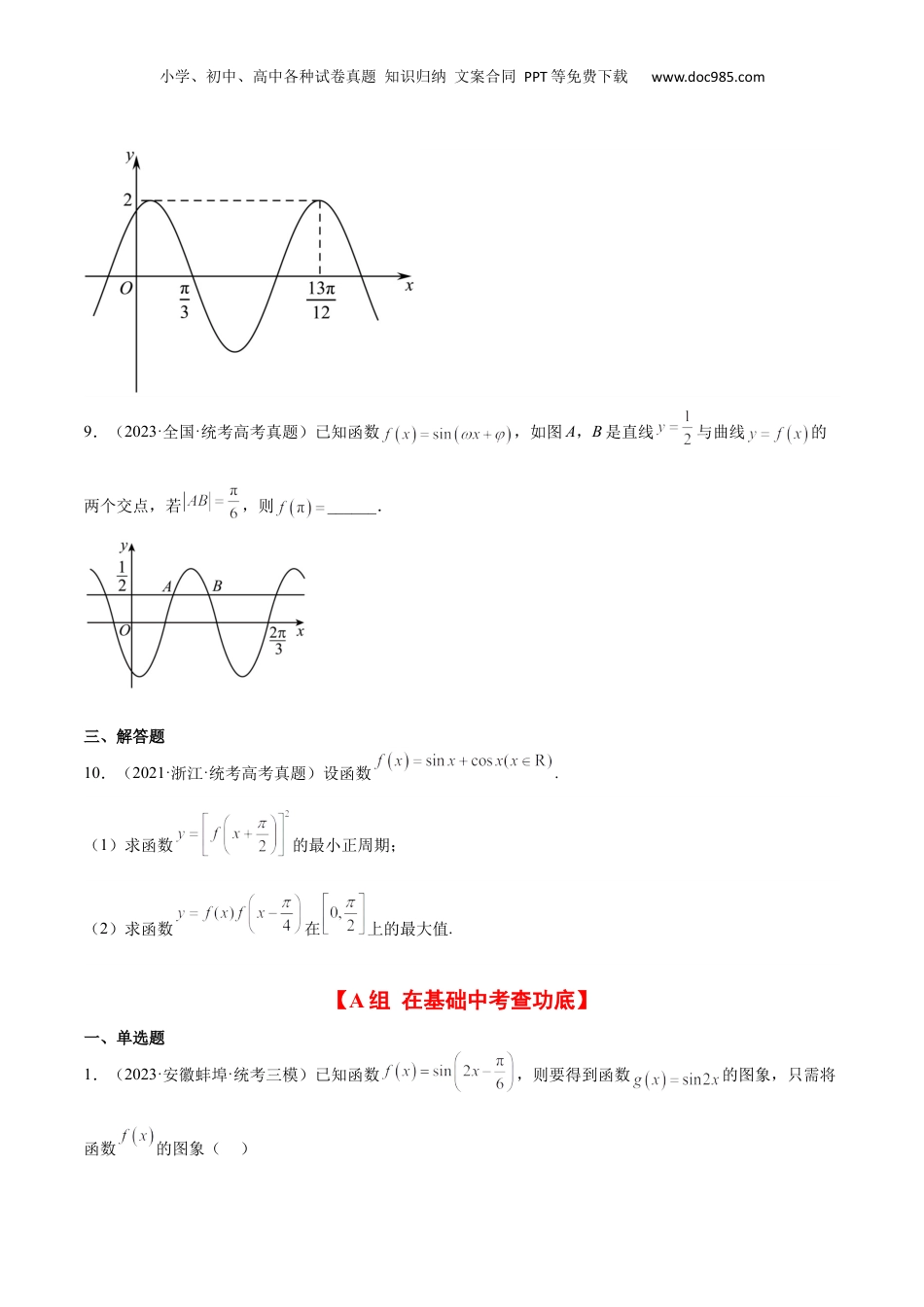
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）第21练函数y＝Asin(ωx＋φ)的图象性质及其应用（精练）一、单选题1．（2022·浙江·统考高考真题）为了得到函数的图象，只要把函数图象上所有的点（）A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度2．（2021·全国·统考高考真题）把函数图像上所有点的横坐标缩短到原来的倍，纵坐标不变，再把所得曲线向右平移个单位长度，得到函数的图像，则（）A．B．C．D．3．（2022·全国·统考高考真题）将函数的图像向左平移个单位长度后得到曲线C，若C关于y轴对称，则的最小值是（）A．B．C．D．4．（2022·全国·统考高考真题）记函数的最小正周期为T．若，刷真题明导向小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com且的图象关于点中心对称，则（）A．1B．C．D．35．（2023·全国·统考高考真题）已知为函数向左平移个单位所得函数，则与的交点个数为（）A．1B．2C．3D．46．（2023·全国·统考高考真题）已知函数在区间单调递增，直线和为函数的图像的两条对称轴，则（）A．B．C．D．7．（2023·天津·统考高考真题）已知函数的一条对称轴为直线，一个周期为4，则的解析式可能为（）A．B．C．D．二、填空题8．（2021·全国·高考真题）已知函数的部分图像如图所示，则_______________.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com9．（2023·全国·统考高考真题）已知函数，如图A，B是直线与曲线的两个交点，若，则______．三、解答题10．（2021·浙江·统考高考真题）设函数.（1）求函数的最小正周期；（2）求函数在上的最大值.【A组在基础中考查功底】一、单选题1．（2023·安徽蚌埠·统考三模）已知函数，则要得到函数的图象，只需将函数的图象（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位2．（2023·河南郑州·模拟预测）把函数图象上所有点的纵坐标不变，横坐标伸长到原来的2倍，再把所得曲线向右平移个单位长度，得到函数的图象，则（）A．B．C．D．3．（2023·福建南平·统考模拟预测）已知函数的图象的相邻两条对称轴间的距离为，则（）A．的周期为B．在上单调递增C．的图象关于点对称D．的图象关于直线对称4．（2023·全国·模拟预测）将函数的图象上各点向右平移个单位长度得函数的图象，则的单调递增区间为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．5．（2023·四川南充·统考三模）已知点是函数的一个对称中心，则为了得到函数的图像，可以将图像（）A．向右平移个单位，再向上移动1个单位B．向左平移个单位，再向上移动1个单位C．向右平移个单位，再向下移动1个单位D．向右平移个单位，再向下移动1个单位6．（2023·河北石家庄·统考三模）已知函数的部分图象如图所示，则图象的一个对称中心是（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com7．（2023·四川·四川省金堂中学校校联考三模）已知直线是函数图象的任意两条对称轴，且的最小值为，则的单调递增区间是（）A．B．C．D．8．（2023·浙江绍兴·统考模拟预测）若函数的周期为，其图象由函数的图象向左平移个单位得到，则的一个单调递增区间是（）A．B．C．D．9．（2023·四川遂宁·统考三模）已知函数，，，且的最小值为，则的值为（）A．B．C．1D．210．（2023·山东烟台·统考二模）已知函数在上单调递增，则的取值范围为（）．A．B．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．D．11．（2023·河北沧州·统考模拟预测）已知函数的图象关于对称，当的最小正周期取得最大值时，距离原点最近的对称中心为（）A．B．C．D．12．（2023·河南鹤壁·鹤壁高中校考模拟预测）已知函数，则下列说法正确的为（）A．的最小正周...