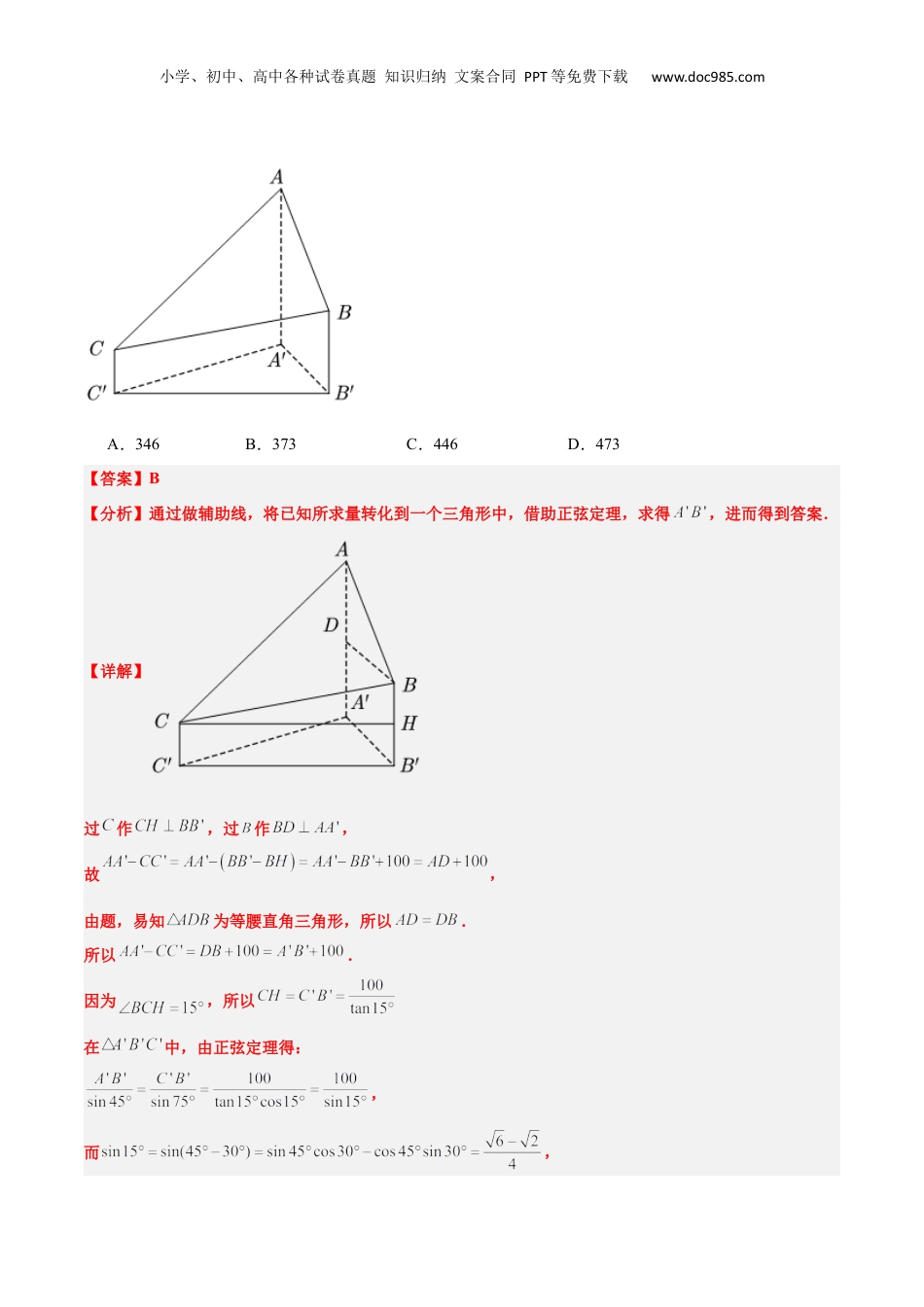
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）第25练解三角形（精练）一、单选题1．（2021·全国·高考真题）在中，已知，，，则（）A．1B．C．D．3【答案】D【分析】利用余弦定理得到关于BC长度的方程，解方程即可求得边长.【详解】设，结合余弦定理：可得：，即：，解得：（舍去），故.故选：D.【点睛】利用余弦定理及其推论解三角形的类型：(1)已知三角形的三条边求三个角；(2)已知三角形的两边及其夹角求第三边及两角；(3)已知三角形的两边与其中一边的对角，解三角形．2．（2021·全国·统考高考真题）魏晋时刘徽撰写的《海岛算经》是有关测量的数学著作，其中第一题是测海岛的高．如图，点，，在水平线上，和是两个垂直于水平面且等高的测量标杆的高度，称为“表高”，称为“表距”，和都称为“表目距”，与的差称为“表目距的差”则海岛的高（）刷真题明导向小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．表高B．表高C．表距D．表距【答案】A【分析】利用平面相似的有关知识以及合分比性质即可解出．【详解】如图所示：由平面相似可知，，而，所以，而，即＝．故选：A.【点睛】本题解题关键是通过相似建立比例式，围绕所求目标进行转化即可解出．3．（2021·全国·统考高考真题）2020年12月8日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86（单位：m），三角高程测量法是珠峰高程测量方法之一．如图是三角高程测量法的一个示意图，现有A，B，C三点，且A，B，C在同一水平面上的投影满足，．由C点测得B点的仰角为，与的差为100；由B点测得A点的仰角为，则A，C两点到水平面的高度差约为（）（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．346B．373C．446D．473【答案】B【分析】通过做辅助线，将已知所求量转化到一个三角形中，借助正弦定理，求得，进而得到答案．【详解】过作，过作，故，由题，易知为等腰直角三角形，所以．所以．因为，所以在中，由正弦定理得：，而，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以所以．故选：B．【点睛】本题关键点在于如何正确将的长度通过作辅助线的方式转化为．二、填空题4．（2021·全国·统考高考真题）记的内角A，B，C的对边分别为a，b，c，面积为，，，则________．【答案】【分析】由三角形面积公式可得，再结合余弦定理即可得解.【详解】由题意，，所以，所以，解得（负值舍去）.故答案为：.5．（2023·全国·统考高考真题）在中，，的角平分线交BC于D，则_________．【答案】【分析】方法一：利用余弦定理求出，再根据等面积法求出；方法二：利用余弦定理求出，再根据正弦定理求出，即可根据三角形的特征求出．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【详解】如图所示：记，方法一：由余弦定理可得，，因为，解得：，由可得，，解得：．故答案为：．方法二：由余弦定理可得，，因为，解得：，由正弦定理可得，，解得：，，因为，所以，，又，所以，即．故答案为：．三、解答题6．（2021·天津·统考高考真题）在，角所对的边分别为，已知，．（I）求a的值；（II）求的值；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（III）求的值．【答案】（I）；（II）；（III）【分析】（I）由正弦定理可得，即可求出；（II）由余弦定理即可计算；（III）利用二倍角公式求出的正弦值和余弦值，再由两角差的正弦公式即可求出.【详解】（I）因为，由正弦定理可得，，；（II）由余弦定理可得；（III），，，，所以.7．（2022·浙江·统考高考真题）在中，角A，B，C所对的边分别为a，b，c．已知．(1)求的值；(2)若，求的面积．【答案】(1)；(2)．【分析】（1）先由平方关系求出，再根据正弦定理即可解出；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）根据余弦定理的推论以及可解出，即可由三角形面积公式求出面积．【详解】...